Project Highlight Slides
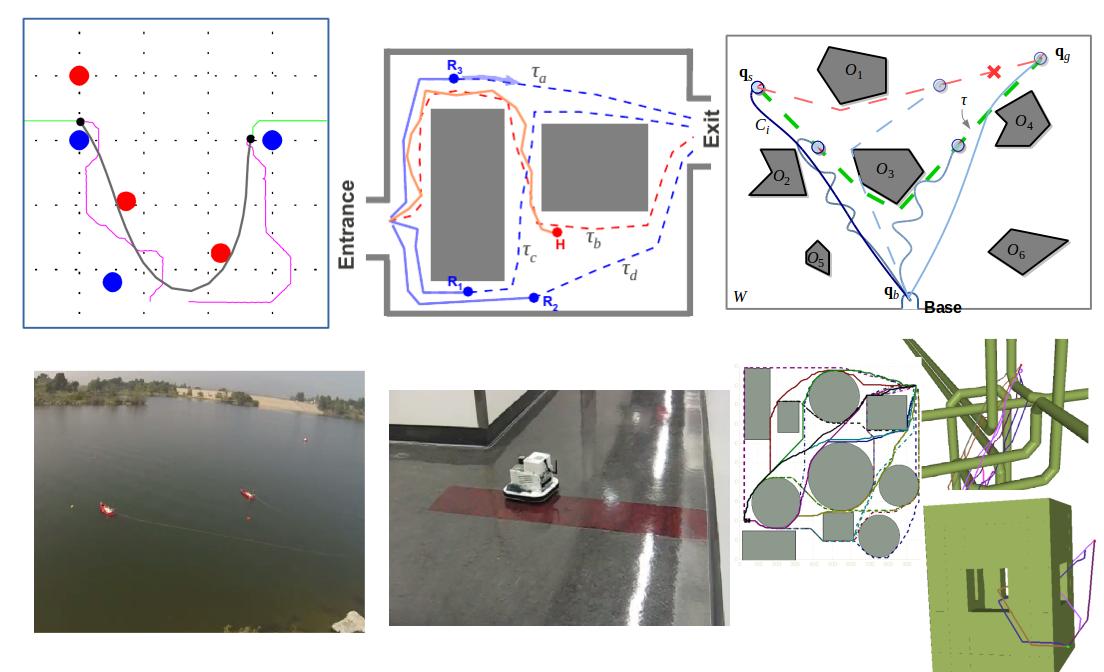
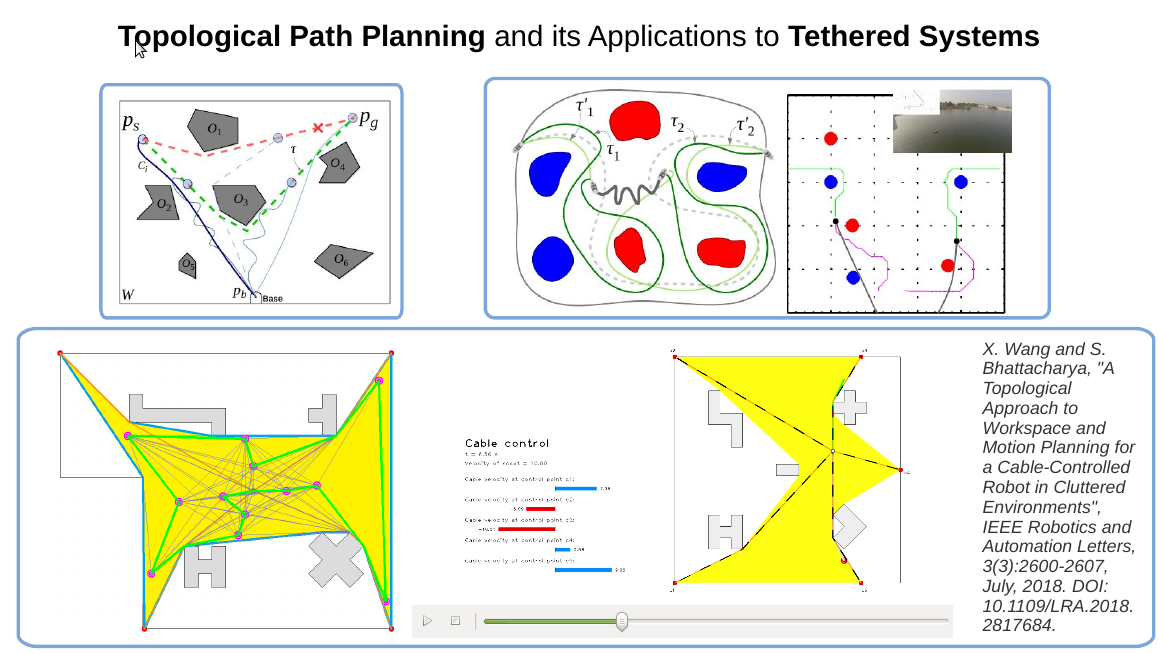
Topological Path Planning (TPP)
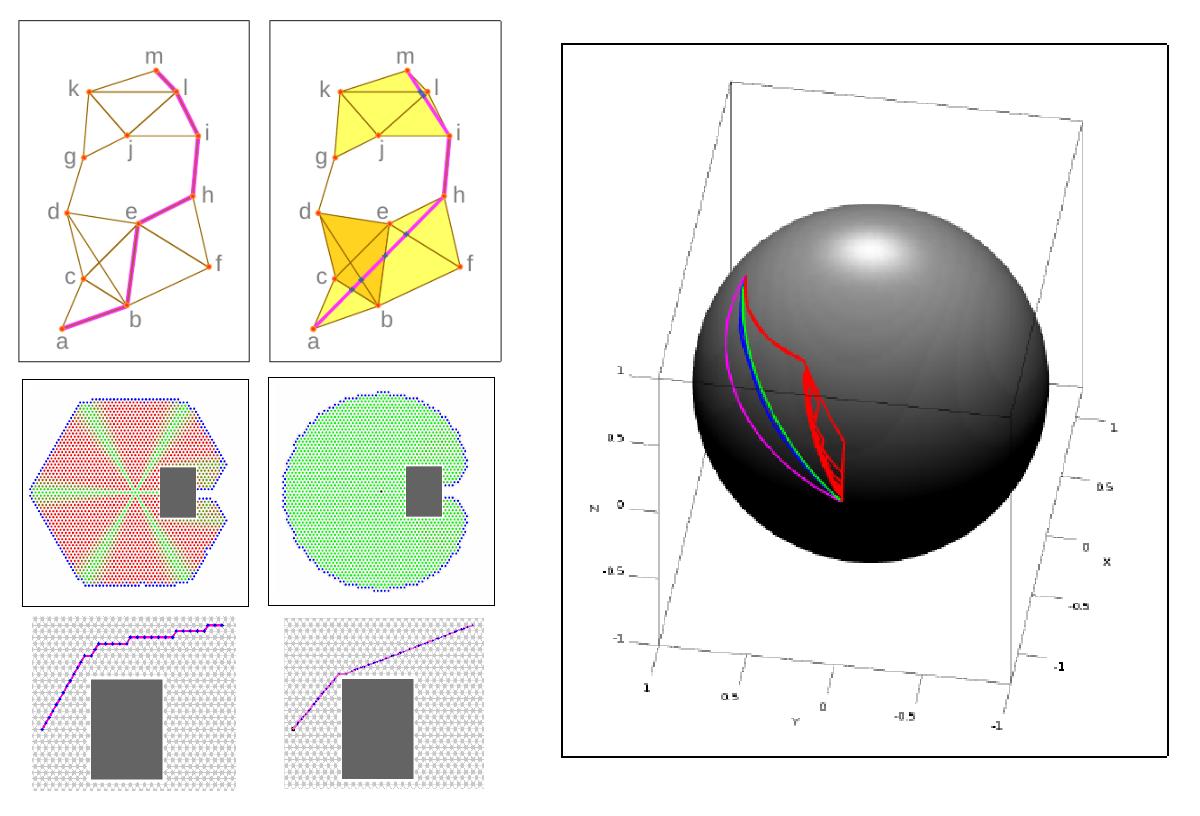
We use topological invariants (homotopy and homology invariants) to augment graph search-based path planning algorithms in order to find optimal paths in different homotopy/homology classes. This lets us solve optimal motion planning for systems involving cables as well as problems such as multi-robot topological exploration.
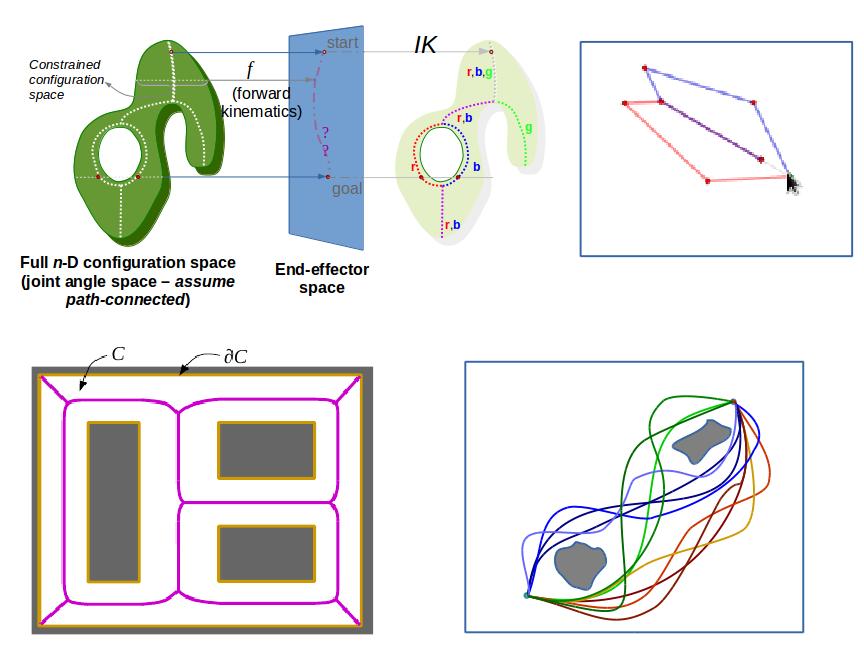
Various topological invariants are used to classify configurations of systems into equivalent classes such that the dimensionality, and hence the complexity, of the system is reduced due to the classification, yet properties such as optimality and algorithmic completeness can be guaranteed even when planning motion in the reduced (quotient) space. Homotopy and homology are useful in classifying trajectories or configuration of flexible cables. More involved constructions such as Reeb graphs are necessary for systems such as robotic arm/manipulator.
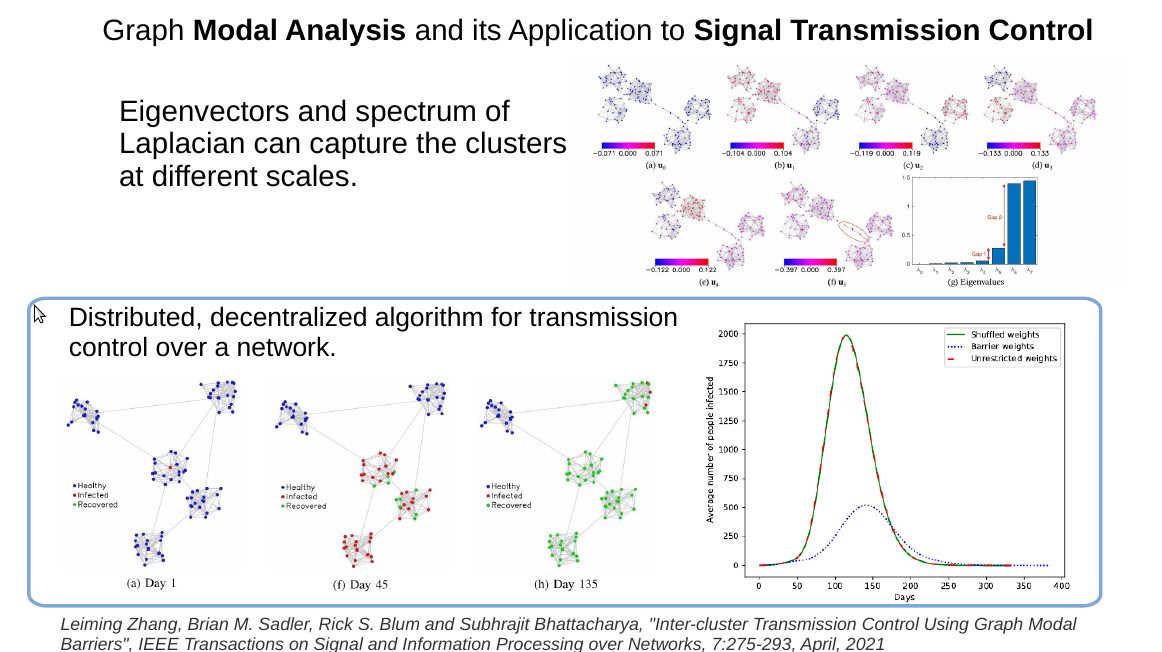
Control of Networked Systems
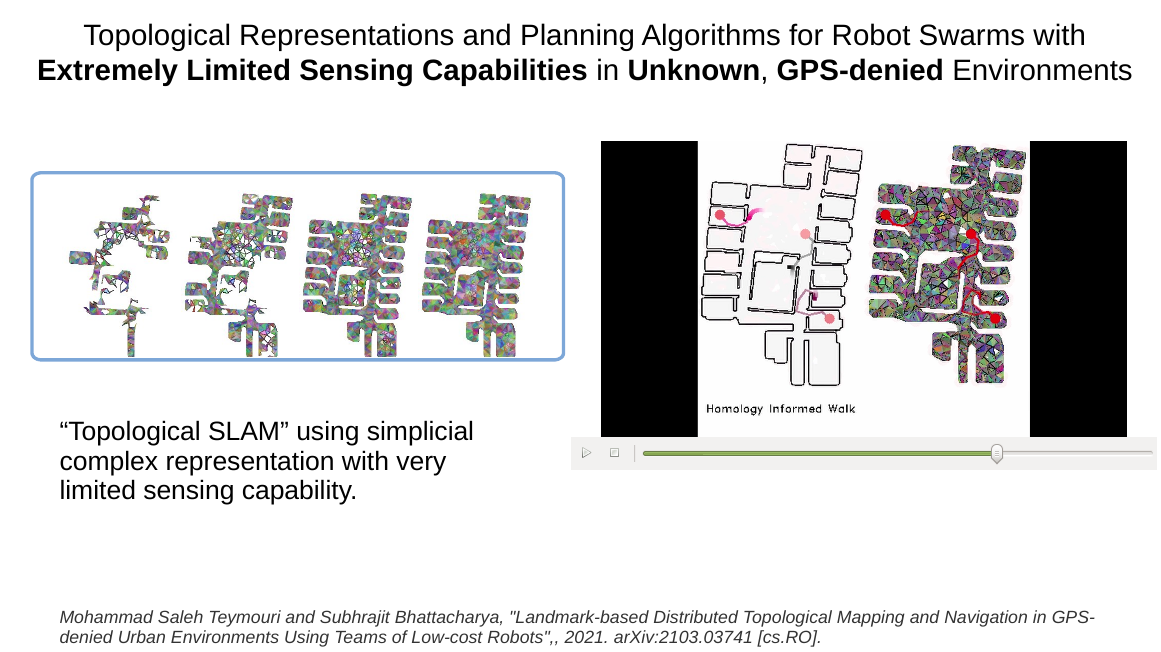
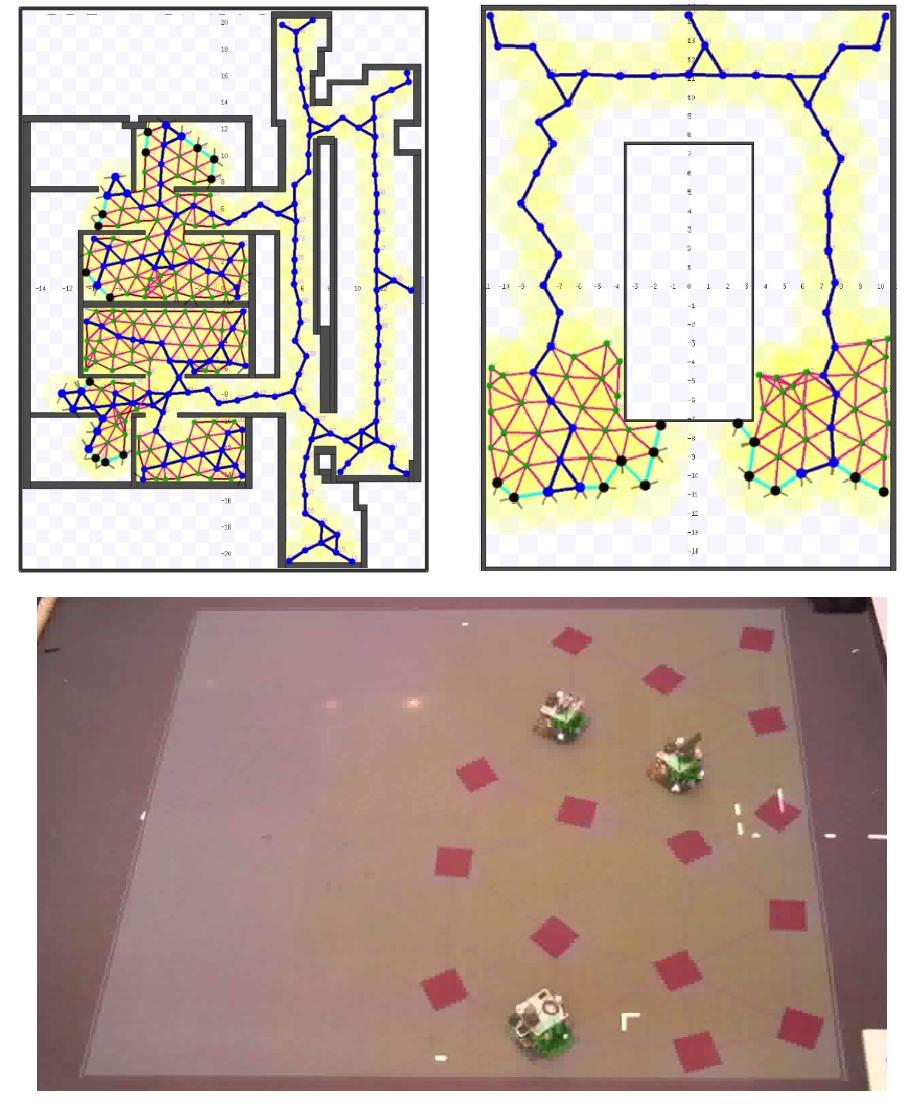
Simplical Representation for Topological Mapping and Path Planning
We are looking into the problem of representing unknown environments without global localization (GPS-denied) using swarms of robots with limited-capability sensors and/or sparsely placed landmark. The application of this research includes mapping of remote, unknown environments, deploying resources in them, and persistent surveillance of such environments.
We are developing analogs of graph search algorithms for finding shortest paths in simplicial complexes. Very often (for example, in optimal motion planning in flows) the shortest path problem can be posed in form of a differential equation. For such problems we are using a finite element-type methods on a simplicial complex representation of the environments in order to solve the differential equations and compute optimal paths.