Special Topics in Applied Mathematics: Introduction to Topology and Differential Geometry for Application in Robotics (Fall 2014, UPenn)
Aug 19, 2014
This is a course on applied mathematics for students in robotics, networking, and distributed systems who are interested in applications of topology and geometry to engineering problems. It is open to all doctoral students in engineering.
Class Schedule
Meeting: 2 meetings/week, 1.5 hours/meeting
Days and time: Tuesdays and Thursdays, 1:30pm - 3:00pm
(Meetings start on Thursday, Sept 4)
Location: Levine 612
Instructor
Subhrajit Bhattacharya, Post doctoral fellow, Department of Mathematics.
e-mail: subhrabh@math.upenn.edu
Office hours: Wednesdays 1-2pm, in DRL room 3C7.
Registering for the Class
You'll need to register for MEAM 899 (PhD Independent Study) or MEAM 599 (MSE Independent Study). Please use section #008 (Prof. Vijay Kumar), since MEAM independent studies need to be under a faculty member. E-mail subhrabh@math.upenn.edu in case of any question.
Texts/Required Materials
Recommended Books:
- James Munkres, "Topology", Prentice Hall, 1999.
- Robert Ghrist, "Elementary Applied Topology".
- Allen Hatcher, "Algebraic Topology", Cambridge Univ. Press, 2001.
- John M. Lee, "Riemannian Manifolds: An Introduction to Curvature", Springer, 1997.
[ + ] Additional Reading and Research Articles.
Description
This course introduces 2nd year engineering graduate students to topology and differential geometry. Basic concepts from topology and Riemannian geometry, including configuration spaces, topology, maps, homotopy, covering spaces, manifolds, atlases, tangent/cotangent spaces, tensor fields, Riemannan metric and curvature will be covered. Tools from algebraic topology, including chain complexes and homology computation, and from differential geometry, including Riemannian metric and the geodesic equation, will be introduced. Definitions from set theory, topology and basic algebraic structures (groups, rings, modules, algebras) will be covered during the course. Focus will be given on the conceptual and application aspects more than formal proofs. Applications from robot motion planning, robot control and sensing, and sensor networks will ground the basic concepts, and students will pursue independent projects with the goal of producing papers that are similar in scope to conference submissions by the end of the course.
Course Objectives
The goal of this course is to expose students to topics in modern mathematics that have turned out to be extremely useful in engineering applications in recent years, but not formally introduced in engineering curriculum. In particular, topics from topology and differential geometry will be introduced, with special emphasis on application and computational aspects. This will require students to:
- Get familiarized with modern mathematical terminologies, notations and concepts from topology and differential geometry, enabling them to effectively communicate with and conduct research in the fields and their applications,
- Learn about computational tools from algebraic topology, their cutting-edge applications in the field of robotics and hand-on experience of solving problems with them,
- Learn about concepts and tools from Riemannian Geometry, with special emphasis on computation and application to robot path planning and coverage problems,
- Get introduced to elementary Lie theory and Bundle theory,
- Learn about basic algebraic structures (groups, rings, modules, algebra, fields, etc.) during the course.
Syllabus and Detailed Weekly Meeting Schedule (Tentative)
Topology (point-set, algebraic and differential):
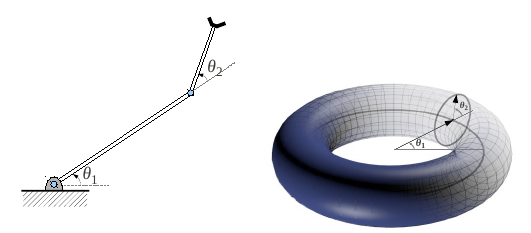
Week 1: Intro to point-set topology: Motivation from robot configuration space (abstract config. space, 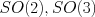 , etc) -- introduce groups and Lie groups; Definitions: Topology, continuous function, homeomorphism, embedding, immersion (with examples from configuration spaces); Quotient space: Construction of one topological spaces from other: Gluing (example: representation of torus, klein bottle, sphere,
, etc) -- introduce groups and Lie groups; Definitions: Topology, continuous function, homeomorphism, embedding, immersion (with examples from configuration spaces); Quotient space: Construction of one topological spaces from other: Gluing (example: representation of torus, klein bottle, sphere,  , etc); Definitions: Homotopy, isotopy (example: homotopic trajectories, knots); Covering spaces (with examples from configuration spaces).
, etc); Definitions: Homotopy, isotopy (example: homotopic trajectories, knots); Covering spaces (with examples from configuration spaces).
Application: Homotopy classes of robot trajectories, Configuration space of simple linkages and multi-robot systems.
Week 2: Definitions: Manifolds, manifolds with boundary (with examples); coordinate charts, atlases (with examples), introduction to tangent space; Cartesian product of spaces (simple examples).
Application: Configuration spaces of simple systems (multi-segment robot arms, linkages, multiple mobile robot/sensor systems with constraints, normalized 3x3 image space, etc) -- i. construct embeddings in higher dimensional Euclidean space, ii. construct atlases on the configuration spaces.
Week 3: Motivation for algebraic topology: Why do we need this? - to be able to do computation; to obtain global information from local information; Introduction: Intro to chain complexes -- Simplicial complex (illustrate with simple example), cellular complex, delta complex (use example of torus - illustrates computation of homology of torus later); Quick review of linear algebra (with emphasis on linear transformation and kernel) -- Gearing up for Homology of a chain complex.
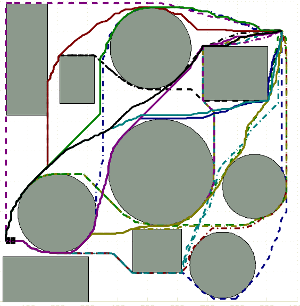
Application: The Cech and Rips complex of sensor covers in a sensor network and how they represent "holes" in coverage.
Week 4: Homology of a chain complex -- computation and interpretation; General description of a chain complex with coefficients in arbitrary groups; Maps between topological spaces inducing maps between homology groups (functoriality of homology); Example: Use Z-coefficient homology computation to show the impossibility in creating continuous maps between some pairs of spaces (e.g.,  and
and 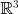 ).
).
Application: Identification of "holes" in sensor network coverage (using Cech ad Rips complex).
Week 5: Quick introduction to cohomology; From discrete to continuous: Singular chain complex, Differential forms and De Rham cohomology; Long exact sequence and a few applications (if time permits).
Application: Use of De Rham cohomology for robot path planning with topological reasoning.
Differential Geometry:
Week 6: Define a "metric" on a topological space. Motivation for Riemannian geometry: Riemannian geometry studies a specific type of metric on manifolds; Definitions: Tangent space, cotangent space, vector fields, covector fields, respective transformations on coordinate changes, tensors and tensor fields, Einstein summation convention.
Application: Example of Manhatan metric vs. Euclidean metric for finding shortest path in an urban environment; Great circles on the surface of Earth for flight/ship navigation -- gearing up for Riemannian metric.
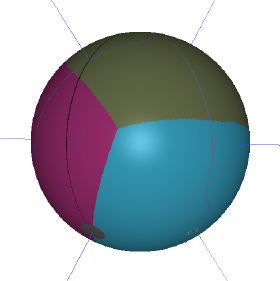
Week 7: Definition: Riemannian metric tensor; Length of smooth curves; Metric induced on a manifold from ambient (space in which immersed) metric; Higher dimensional measures derived from Riemannain metric, Volume form; Covariant derivative, Geodesics, geodesic equation, affine connections, Christoffel symbols, Exponential maps; Exercise/example: Numerically compute a geodesic (with given initial point and tangent) given the Riemannian metric in a coordinate chart; Exercise/example: Numerically compute volume given the metric. Compute generalized centroid of a subset.
Application: Multi-robot coverage problem using a generalized Lloyd's algorithm on Riemannian manifolds.
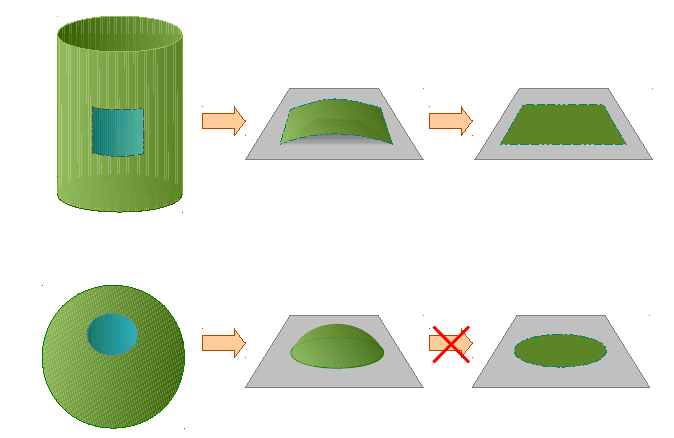
Week 8: General definition/interpretation of Affine connections. Introduction to Parallel transport, curvature; Affine connections and geodesics on a manifold without a Riemannian metric (example: using affine connection induced by right/left actions on Lie groups); Definition and interpretation of torsion tensor, curvature of affine connection.
Application: Notion of "shortest" paths on config. space of some systems which are also Lie groups (e.g., n-segmented robot arm), whithout having to introduce a Riemannian meric.
Elementary Lie Theory:
Week 9: Revisit Lie groups with simple examples relevant to robotics (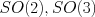 ); Lie algebra (motivated from Lie groups), lie brackets, connection between Lie groups & algebra (commutativity, subgroup/subalgebra); Exponential map; Construction of Lie group (up to a cover) from a given Lie algebra: e.g.,
); Lie algebra (motivated from Lie groups), lie brackets, connection between Lie groups & algebra (commutativity, subgroup/subalgebra); Exponential map; Construction of Lie group (up to a cover) from a given Lie algebra: e.g.,  vs
vs 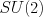 ; Introduction to representations.
; Introduction to representations.
Application: Rotation groups and non-commutativity of  , infinitesimal rotation.
, infinitesimal rotation.
Week 10: Review of definition of algebra over a field; Review matrix algebra and the group structure on invertible matrices; Introduction to representations of Lie groups and algebra (with examples); Introduction to classification of semi-simple and simple lie algebra; Vector fields as Lie algebra of automorphism groups; Lie brackets of vector fields.
Application: Representation of infinitesimal rotations; Pairs of vector fields on a manifold (for example, for robot navigation) which commute and which do not commute, and the implication of that.
Elementary Bundle Theory:
Week 11: Motivating for bundle theory with examples -- Mobius band vs the cylinder, torus vs klein bottle; Definitions: Fiber bundles, clutching function, vector bundle; Definition: Tangent bundle (with examples of vector bundles that are tangent bundles, and which are not); Vector fields revisited.
Application: Identifying local product structure in some configuration spaces and figuring out if the local product structure extends globally (e.g., 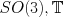 , etc.).
, etc.).
Week 12: Pullback bundle; Basic theorems involving pullbacks, homotopy equivalent base spaces, etc.; Example: Hairy ball theorem with simple proof (introduce concept of "topological obstruction"); A hint of classifications of bundles.
Application: Axis-angle representation of the double cover of  -- not a homeomorphism with
-- not a homeomorphism with 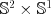 -- Introduction to Hopff fibration.
-- Introduction to Hopff fibration.
Week 13: Final Presentation of Term Project


