We have established a research group at Lehigh University focusing on assessment and enhancement of Community Resilience, Infrastructure Reliability, and Life-Cycle Sustainability. This is achieved advancing the state-of-the-art in Computational Mechanics, Probabilistic Modeling and Simulation, Operational Research, High Performance Computing and Big Data Analysis.
This page provides an overview of the current research efforts. Additional information is available at the pages dedicated to our publications and software.
Probabilistic Resilience Assessment of Interdependent Systems (PRAISys)
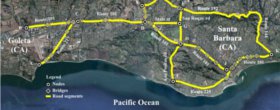
The Probabilistic Resilience Assessment of Interdependent Systems (PRAISys) project is a multi-million dollar effort sponsored by the National Science Foundation, which has run for 5 years, involving more than 50 different scholars in 6 departments across engineering and social sciences. The project aims at developing a simulator that can predict the damage caused by an extreme event on the infrastructure systems of a region, the subsequent decision making and the resulting recovery. The platform focuses on hurricanes and earthquakes acting on transportation, power, and communication infrastructure. The project emphasizes the important of accounting for uncertainties throughout the process, as well as for interdependencies among various components of a system, and across systems. More information is available on the official website: www.praisys.org
Most representative publication:

Wenjuan Sun, Paolo Bocchini, Brian D. Davison.
Resilience metrics and measurement methods for transportation infrastructure: The state of the art.
Sustainable and Resilient Infrastructure, Taylor and Francis, in press and available online.
DOI: 10.1080/23789689.2018.1448663
Non-homogeneous virus spreading and associated large-scale risk
The main goal of this project is to increase the ability to forecast zoonotic disease outbreaks and take informed decisions to prevent or at least mitigate such outbreaks. The effort includes the development of a rigorous framework that combines models of environmental and ecological conditions, migration pattern and behavior of the animal host, disease cycles in the host and humans, socio-economic factors that influence the transmission of the disease to humans, and socio-economic consequences of human disease contraction. The project is a collaborative work of multiple investigators, with expertise in probabilistic modeling, regional analysis, disease spreading, and health-related socio economic analysis. Some preliminary results have been obtained through a COllaborative REsearch (CORE) grant provided by Lehigh University. The project was supported by the National Institute of Health. More information on the NIH sponsored portion is available at go.lehigh.edu/pareo.
Most representative publication:

Graziano Fiorillo, Paolo Bocchini, Javier Buceta.
A predictive spatial distribution framework for filovirus-infected fruit bats.
Scientific Reports, Nature, Vol. 8, Article 7970, p. 1-13, 2018.
DOI: 10.1038/s41598-018-26074-4
Multi-Hazard Quantization
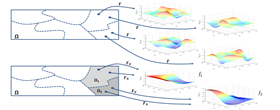
The risk from natural hazards for a specific region is usually assessed predicting the losses associated with a set of representative extreme event scenarios. The selection of these scenarios is extremely delicate, because computational resources typically constrain heavily the number of cases that can be investigated. Hence, the selected scenarios have to be as few as possible, and yet provide a comprehensive probabilistic description of the regional hazard. The investigators have developed a technique called "Hazard Quantization" (HQ) to achieve this goal, but it falls short when there is the need to describe multiple hazards occurring simultaneously, such as strong hurricane winds and storm surge. This project will investigate a new methodology that can capture simultaneously multiple hazard intensity measures spread over a region. The team includes experts in stochastic modeling of random functions and experts in analysis of regional natural hazards. The project will result in a new approach grounded in solid mathematics, that will yield substantial enhancements in the computational efficiency of these analyses, enabling their applicability to practical-size problems and, ultimately, advancing disaster mitigation and response. The project is currently supported by an Accelerator grant provided by Lehigh University.
Most representative publication:

Vasileios Christou, Paolo Bocchini, Manuel J. Miranda, Aman Karamlou.
Effective sampling of spatially correlated intensity maps using Hazard Quantization: application to seismic events.
Journal of Risk and Uncertainty in Engineering Systems, Part A: Civil Engineering, ASCE - ASME, Vol. 4, Issue 1, p. 04017035 1-13, 2017.
DOI: 10.1061/AJRUA6.0000939
3D-Printing Concrete by Selective Binder Activation

The team has developed a manufacturing process that can 3D print cementitious objects using a methodology called "3D printing by selective binder activation". The objects can be produced with any shape, including overhangs and voids that are difficult or impossible to achieve with other approaches. The resulting artifacts have good geometric accuracy and mechanical characteristics relatively close to those of cast-in-place concrete. Innovative approaches are being used also to integrate reinforcement. Finally, new techniques for multi-material topology optimization are being developed to take full advantage of these new manufacturing capabilities.
This project is partially funded by and completed in collaboration with Buzzi Unicem USA. Additional funding is provided by the Pennsylvania Department of Comunity and Economic Development. The project is a collaboration among the research teams of Dr. Bocchini (PI), Dr. Naito, and Dr. Fox.
Most representative publication:

Joseph Ingaglio, John Fox, Clay J. Naito, Paolo Bocchini.
Material characteristics of binder jet 3D printed hydrated CSA cement with the addition of fine aggregates.
Construction and Building Materials, Elsevier, Vol. 206, p. 494-503, 2019.
DOI: 10.1016/j.conbuildmat.2019.02.065
Life-Cycle FEM
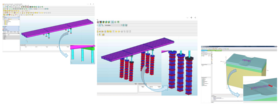
There are numerous examples in the literature of the benefits of advanced numerical modeling (e.g. FE analysis) towards a better and more robust structural assessment of Civil Engineering structures. Nevertheless, this type of modeling involves substantial investments in terms of time, as well as qualified experts to conduct the required work. In such context, the Life-Cycle FEM analysis group aims to better understand the implications of such investments, as well as their relevance, in the context of the Life-Cycle analysis of engineering structures. This would be an important step forward towards a holistic approach to asset management of engineering structures, which is perfectly in line with the Sustainable Development Goals defined in the 2030 Agenda for Sustainable Development (United Nations 2015). More information is available on the official website: go.lehigh.edu/lifecyclefem
Most representative publication:

12th International DIANA Users Meeting
Porto, Portugal, October 11-12, 2018
Ali Wazeer, Helder Sousa, Paolo Bocchini
FE modelling approaches for soil-bridge systems towards better emergency response planning.
In Proceedings of the 12th International DIANA Users Meeting, 2018.
