Background

I am currently a Professor of Applied Mathematics at Department of Mathematics, Lehigh University. I am also affiliated with the College of Health and the Institute for Data, Intelligent Systems, and Computation (I-DISC) at Lehigh.

My research is centered around scientific machine learning (SciML) and numerical analysis for high-order methods, and in particular how to obtain useful mathematical and numerical models of complex physical and biological systems. I am particularly interested in applying the mathematical analysis knowledges in the design and analysis of mathematical models and numerical schemes.

Quick links:

My Curriculum Vitae: .pdf

My Google Scholar page: .html

Research Interests

My research interests include:

Scientific Machine Learning: - Nonlocal Neural Operator Learning; - Graph Neural Networks (GNN); - Causal Inference
High-Order Methods: - Meshfree Methods; - Spectral Element Methods; - Isogeometric Analysis (IGA)
Multiscale/Multiphysics Problems: - Fluid--Structure Interaction; - Local-Nonlocal Coupling Problems; - Peridynamics and Other Nonlocal Models
Modeling for Real-World Applications: - Materials; - Soft Tissues; - Natural Language Processing

Education

2014

Ph.D.

Brown University

Applied Mathematics

Thesis: Numerical methods for fluid-structure interactions: analysis and simulations

2013

M.Sc.

Brown University

Mechanical Engineering (Solid Mechanics)

2008

B.S.

Peking University

Mathematics

Contact Information

Name:

Yue Yu

Email:

yuy214 [at] lehigh [dot] edu

Office:

Chandler Ullmann Hall, Room 243

Phone:

610-758-3752

Mailing Address:

Lehigh University, Bethlehem, PA, 18015

Education and Academic Experience

Since Jul. 2023

Professor

Department of Mathematics, Lehigh University

Since Mar. 2022

Affiliated Faculty

The College of Health, Lehigh University

Since Sep. 2018

Affiliated Faculty

Institute for Data, Intelligent Systems, and Computation (I-DISC), Lehigh University

Nov. 2023-Dec. 2023

IBM Visiting Professor

Division of Applied Mathematics, Brown University, USA

Host: Prof. George Karniadakis

Jul. 2019-Jun. 2023

Associate Professor

Department of Mathematics, Lehigh University

Aug. 2014-Jun. 2019

Tenure-Track Assistant Professor

Department of Mathematics, Lehigh University

Feb. 2017-Mar. 2017

Visiting Professor

Institute for Computational Engineering and Sciences, The University of Texas at Austin, USA

Host: Prof. Thomas J.R. Hughes

2014-2016,

Visiting Scholar

each summer

Mathematics Group, Lawrence Berkeley National Laboratory, USA

Host: Prof. James Sethian

Jun. 2014-Jul. 2014

Postdoc Fellowship

School of Engineering and Applied Science, Harvard University, USA

Adviser: Prof. Chris Rycroft

Sep. 2008-May. 2014

Ph.D. in Applied Mathematics

Division of Applied Mathematics, Brown University, USA

Adviser: Prof. George E. Karniadakis

Sep. 2008-May. 2013

M.Sc. in Mechanical Engineering (Solid Mechanics)

School of Engineering, Brown University, USA

Feb. 2012-Apr. 2012

Visiting Graduate Student

School of Mechanical Engineerin, University of Campinas, Brazil

Prof. Marco L. Bittencourt

Sep. 2004-Jul. 2008

B.Sc. in Mathematics

School of Mathematics, Peking University, China

Adviser: Prof. Huazhong Tang

Fellowships, Honors and Awards

2023

IBM Visiting Faculty Fellowship, Brown University

2022

Recognition for Outstanding Academic Achivement, Lehigh University

2022

Air Force Young Investigator

2021

NSF-MAPWISELY Faculty Success Fellowship

2018

National Science Foundation CAREER Award

2017,2018

Class of 1968 Junior Faculty Fellowship, Lehigh University

2015

Travel Award, The International Council for Industrial and Applied Mathematics (ICIAM)

2014

AWM-NSF Travel Award, Association for Women in Mathematics (AWM)

2014

Dunmu Ji Thesis Award, Brown University

2012-2013

Simon Ostrach Fellowship, Brown University

2008-2009

Graduate Fellowship, Brown University

2007

Southwest Education Fellowship, Peking University

2005, 2006

Mary Kay Education Fellowship, Peking University

2004

New Student Fellowship, Peking University

2004

Silver Medal in Chinese Mathematical Olympiad, China

Courses Taught

Lehigh University

Math450: Numerical PDEs

Math409: Topics in Numerical Analysis

Math341: Mathematical Models and Their Formulation

Math230: Numerical Methods

Math205: Linear Methods

Math023: Calculus III

Brown University

APMA0330: Methods of Applied Mathematics I

APMA0340: Methods of Applied Mathematics II

Selected Professional Activities

2022 - present

Associate Editor: Advances in Computational Science and Engineering (ACSE)

2022 - present

Editorial Board Member: Computer Methods in Applied Mechanics and Engineering (CMAME), (Nature) Scientific Reports, Numerical Methods for Partial Differential Equations (NMPDE)

2023 - present

Guest Editor: Frontiers in Mechanical Engineering, Special Issue on Hybrid Modeling – Blending Physics with Data

2023 - present

Publicity Officer of the International Association for Computational Mechanics (IACM) Female Researchers Chapter

2022 - present

Vice President of the Society for Industrial and Applied Mathematics (SIAM) NYNJPA Section

2021 - present

Committee member of the Lehigh I-DISC Data and Computing Equity and Justice (DCEJ) Working group

2020 - present

Co-Founder of the One Nonlocal World project and the One Nonlocal World YouTube Channel

2017 - present

Co-Organizer of the Annual High-Performance Computing (HPC) Workshop, Bethlehem, Pennsylvania

2016 - present

Reviewer/Panelist of Funding Agencies: National Science Foundation, National Science Centre in Poland

2015 - present

Member of the Computational Fluid Dynamics and Fluid–Structure Interaction Technical Thrust Area (TTA) Committee of USACM

2018 - 2020

Faculty Advisory Council member of the Lehigh Institute for Data, Intelligent Systems and Computation (I-DISC)

Current Group Members

Shang-Huan Chiu

Email: shc622 [at] lehigh [dot] edu

C.-C. Hsiung Visiting Assistant Professor

Research Interests: Numerical Analysis, Nonlocal Models, Fluid--Structure Interaction

Siavash Jafarzadeh

Email: sij222 [at] lehigh [dot] edu

C.-C. Hsiung Visiting Assistant Professor

Research Interests: Computational Mechanics, Nonlocal Models, Nonlocal Neural Operators

Yiming Fan

Email: yif319 [at] lehigh [dot] edu

Ph.D. candidate in Applied Mathematics

Research Interests: Nonlocal Problems, Uncertainty Quantification

Lu Zhang

Email: luz319 [at] lehigh [dot] edu

Ph.D. candidate in Applied Mathematics

Research Interests: Scientific Machine Learning, Graph Neural Networks, Natural Language Processing

Jiuzhou Chen

Email: jic422 [at] lehigh [dot] edu

Ph.D. candidate in Applied Mathematics

Research Interests: Scientific Machine Learning, Nonlocal Neural Operators

Neeraj Tatikola

Email: nkt222 [at] lehigh [dot] edu

M.Sc. in Applied Mathematics

Research Interests: Scientific Machine Learning, Integral Neural Operators

Former Group Members

Cory Wright

C.-C. Hsiung Visiting Assistant Professor, Lehigh University

Faculty in the Mathematics Department, Milwaukee School of Engineering (MSOE)

Huaiqian You

Ph.D. in Applied Mathematics, Lehigh University

Applied Machine Learning Scientist, Signify N.V.

Josiah Mount

M.Sc. in Applied Mathematics, Lehigh University

Assistant Professor of Mathematics in Northampton Community College

Katherine Wu

M.Sc. in Statistics, Lehigh University

Research Engineer at The Johns Hopkins University Applied Physics Laboratory

Quinn Zhang

B.Sc. in Mathematics, Lehigh University

Ph.D. Student of Applied Mathematics at New York University

Anna Thomas

B.Sc. in Mathematics, Lehigh University

Ph.D. Student of Mathematics at University of Pittsburgh

Mengran He

B.Sc. in Applied Mathematics, Lehigh University

Master Student of Statistical Practice at Carnegie Mellon University

Cianael Paasewe

B.Sc. in Biological Science, Northampton Community College

Awarded as Academic All-Star and member of the All-PA Academic Team by the international honor society Phi Theta Kappa and the Pennsylvania Commission for Community Colleges

Publications and Preprints

Book Chapters

Goswami S, Bora A, Yu Y, Karniadakis G (2023) Physics-informed deep neural operator networks. Machine Learning in Modeling and Simulation: Methods and Applications.
Yu Y (2018) Fluid-structure interaction modeling in 3D cerebral arteries and aneurysms. Lecture Notes in Applied and Computational Mechanics: Biomedical Technology.
Yu Y, Kirby M, Karniadakis GE (2017) Spectral element and hp methods. Encyclopedia of Computational Mechanics.

Publications in Refereed Journals/Conferences

Yin N, Gao T, Yu Y, Ji Q (2024) Effective causal discovery under identifiable heteroscedastic noise model. The 38th AAAI Conference on Artificial Intelligence (AAAI-24).
Liu N, Jafarzadeh S (Postdoc Advisee), Yu Y (2023) Domain agnostic Fourier neural operators. Advances in Neural Information Processing Systems (NeurIPS) 2023.
Zhang L (Ph.D. student), You H (Ph.D. student), Gao T, Yu M, Lee C-H, Yu Y (2023) MetaNO: how to transfer your knowledge on learning hidden physics. Computer Methods in Applied Mechanics and Engineering. 417:116280.
Lu F, An Q, Yu Y (2023) Nonparametric learning of kernels in nonlocal operators. Journal of Peridynamics and Nonlocal Modeling. 1-24.
You H (Ph.D. student), Xu X, Yu Y, Silling S, D'Elia M, Foster J (2023) Towards a unified nonlocal, peridynamics framework for the coarse-graining of molecular dynamics data with fractures. Applied Mathematics and Mechanics. 44, 1125-1150.
Fan Y (Ph.D. student), You H (Ph.D. student), Yu Y (2023) OBMeshfree: An optimization-based meshfree solver for nonlocal diffusion and peridynamics models. Journal of Peridynamics and Nonlocal Modeling. 1-29.
Fan Y (Ph.D. student), D'Elia M, Yu Y, Najm H, Silling S (2023) Bayesian Nonlocal Operator Regression (BNOR): a data-driven learning framework of nonlocal models with uncertainty quantification. ASCE's Journal of Engineering Mechanics. 149(8), 04023049.
Liu N, Yu Y, You H (Ph.D. student), Tatikola N (master student) (2023) INO: invariant neural operators for learning complex physical systems with momentum conservation. Proceedings of The 26th International Conference on Artificial Intelligence and Statistics, PMLR 206:6822-6838.
Silling S, D’Elia M, Yu Y, You H (Ph.D. student), Fermen-Coker M (2023) Peridynamic model for single-layer graphene obtained from coarse grained bond forces. Journal of Peridynamics and Nonlocal Modeling. 5(2), 183-204.
Foss M, Radu P, Yu Y (authors are ordered in alphabetic) (2023) Convergence analysis and numerical studies for linearly elastic peridynamics with Dirichlet-type boundary conditions. Journal of Peridynamics and Nonlocal Modeling. 5(2), 275-310.
You H (Ph.D. student), Zhang Q (undergraduate student), Ross C, Lee C-H, Hsu M-C, Yu Y (2022) A physics-guided neural operator learning approach to model biological tissues from digital image correlation measurements. Journal of Biomechanical Engineering. 144(12), 121012.
Yin M, Zhang E, Yu Y, Karniadakis G (2022) Interfacing finite elements with deep neural operators for multiscale modeling in mechanics. Melosh Medal Competition.
Gao T, Nelson E, Bhattacharjya D, Liu M, Yu Y(2022) IDYNO: learning nonparametric DAGs from interventional dynamic data. International Conference on Machine Learning (ICML) 2022, (pp. 6988-7001). PMLR.
Zhang L (Ph.D. student), You H (Ph.D. student), Yu Y (2022) MetaNOR: A meta-learnt nonlocal operator regression approach for metamaterial modeling. MRS Communications. 12, 662-677.
Fitzpatrick D, Pham K, Ross C, Laurence D, Hudson L, Yu Y, Lee C-H (2022) Ex-vivo experimental characterizations for understanding the interrelationship between tissue mechanics and collagen microstructure of porcine mitral valve leaflets. Journal of the Mechanical Behavior of Biomedical Materials. 134, 105401.
You H (Ph.D. student), Yu Y, D'Elia M, Gao T, Silling S (2022) Nonlocal Kernel Network (NKN): a stable and resolution independent deep neural network. Journal of Computational Physics. 469:111534.
Fan Y (Ph.D. student), You H (Ph.D. student), Tian X, Yang X, Li X, Prakash N, Yu Y (2022) A meshfree peridynamic model for brittle fracture in randomly heterogeneous material. Computer Methods in Applied Mechanics and Engineering. 398:115296.
Tang X, Yu Y, Oztekin A (2022) Asymptotic method for entropic multiple relaxation time model in lattice Boltzmann method. Physical Review E. 106(1), 015303.
Yin M, Zhang E, Yu Y, Karniadakis G (2022) Interfacing finite elements with deep neural operators for fast multiscale modeling of mechanics problems. Computer Methods in Applied Mechanics and Engineering. 402:115027.
Fan Y (Ph.D. student), Tian X, Yang X, Li X, Webster C, Yu Y (2022) An asymptotically compatible probabilistic collocation method for randomly heterogeneous nonlocal problems. Journal of Computational Physics. 465:111376.
You H (Ph.D. student), Zhang Q (undergraduate student), Ross C, Lee C-H, Yu Y (2022) Learning deep implicit Fourier neural operators (IFNOs) with applications to heterogeneous material modeling. Computer Methods in Applied Mechanics and Engineering. 398:115296.
Du Q, Tian X, Wright C (Postdoc Advisee), Yu Y (authors are ordered in alphabetic) (2022) Nonlocal trace spaces and extension results for nonlocal calculus. Journal of Functional Analysis. 282(12), 109453.
Goswami S, Yin M, Yu Y, Karniadakis G (2022) A physics-informed variational DeepONet for predicting the crack path in brittle materials. Computer Methods in Applied Mechanics and Engineering. 391:114587.
You H (Ph.D. student), Yu Y, Silling S, D'Elia M (2022) A data-driven peridynamic continuum model for upscaling molecular dynamics. Computer Methods in Applied Mechanics and Engineering. 389:114400.
D'Elia M, Yu Y (2022) On the prescription of boundary conditions for nonlocal diffusion and peridynamics models. Association for Women in Mathematics Series: Research in the Mathematics of Materials Science
Yu Y, Gao T, Yin N, Ji Q (2021) DAGs with no curl: an efficient DAG structure learning approach. International Conference on Machine Learning (ICML) 2021, (pp. 12156-12166). PMLR.
You H (Ph.D. student), Yu Y, Silling S, D'Elia M (2021) Data-driven learning of nonlocal models: from high-fidelity simulations to constitutive laws. AAAI Spring Symposium: MLPS
Yu Y, You H (Ph.D. student), Trask N (2021) An asymptotically compatible treatment of traction loading in linearly elastic peridynamic fracture. Computer Methods in Applied Mechanics and Engineering. 377:113691.
You H (Ph.D. student), Yu Y, Trask N, Gulian M, D’Elia M (2021) Data-driven learning of nonlocal physics from high-fidelity synthetic data. Computer Methods in Applied Mechanics and Engineering. 374:113553.
D'Elia M, Li X, Seleson P, Tian X, Yu Y (authors are ordered in alphabetic) (2021) A review of Local-to-Nonlocal coupling methods in nonlocal diffusion and nonlocal mechanics. Journal of Peridynamics and Nonlocal Modeling, 1-50.
Zhang L (Ph.D. student), Yu M, Gao T, Yu Y (2020) MCMH: learning multi-chain multi-hop rules for knowledge graph reasoning. KR2ML - Knowledge Representation and Reasoning Meets Machine Learning Workshop.
Yu Y, Gao T (2020) DAGs with no curl: efficient DAG structure learning. NeurIPS Workshop on Causal Discovery and Causality-Inspired Machine Learning.
Wei D, Gao T, Yu Y (2020) DAGs with no fears: a closer look at continuous optimization for learning Bayesian networks. (Spotlight) Advances in Neural Information Processing Systems (NeurIPS) 2020;33.
Zhang L (Ph.D. student), Yu M, Gao T, Yu Y (2020) MCMH: learning multi-chain multi-hop rules for knowledge graph reasoning. Proceedings of the 2020 Conference on Empirical Methods in Natural Language Processing (EMNLP): Findings 2020 (pp. 3948-3954).
D’Elia M, Flores C, Li X, Radu P, Yu Y (authors are ordered in alphabetic) (2020) Helmholtz-Hodge decompositions in the nonlocal framework. Journal of Peridynamics and Nonlocal Modeling. 2(4):401-18.
You H (Ph.D. student), Yu Y, Kamensky D (2020) An asymptotically compatible formulation for local-to-nonlocal coupling problems without overlapping regions. Computer Methods in Applied Mechanics and Engineering. 366:113038.
D'Elia M, Tian X, Yu Y (authors are ordered in alphabetic) (2020) A physically consistent, flexible, and efficient strategy to convert local boundary conditions into nonlocal volume constraints. SIAM Journal on Scientific Computing. 42(4):A1935-49.
You H (Ph.D. student), Lu X, Trask N, Yu Y (2020) An asymptotically compatible approach for Neumann-type boundary condition on nonlocal problems. ESAIM: Mathematical Modelling and Numerical Analysis. 54(4):1373-413.
Rycroft CH, Wu CH, Yu Y, Kamrin K (2020) Reference map technique for incompressible fluid–structure interaction. Journal of Fluid Mechanics. 898.
Yu Y, Chen J, Gao T, Yu M (2019) DAG-GNN: DAG structure learning with graph neural networks. International Conference on Machine Learning (ICML) 2019, (pp. 7154-7163). PMLR.
Trask N, You H (Ph.D. student), Yu Y, Parks ML (2019) An asymptotically compatible meshfree quadrature rule for nonlocal problems with applications to peridynamics. Computer Methods in Applied Mechanics and Engineering, 343:151-65.
Yu Y, Yu Y, Kamensky D, Hsu MC, Lu XY, Bazilevs Y, Hughes TJ (2018) Error estimates for projection-based dynamic augmented Lagrangian boundary condition enforcement, with application to fluid–structure interaction. Mathematical Models and Methods in Applied Sciences, 28(12):2457-509.
Yu Y, Bargos F, You H (Ph.D. student), Bittencourt ML, Parks ML, Karniadakis GE (2018) A partitioned coupling framework for peridynamics and classical theory: analysis and simulations. Computer Methods in Applied Mechanics and Engineering, 340:905-931.
Kamensky D, Hsu M-C, Yu Y, Evans JA, Sacks MS, Hughes TJR (2017) Immersogeometric cardiovascular fluid--structure interaction analysis with divergence-conforming B-splines. Computer Methods in Applied Mechanics and Engineering, 314:408-472.
Schillinger D, Harari I, Hsu M-C, Kamensky D, Stoter SKF, Yu Y, Zhao Y (besides the first author, all other authors are ordered in alphabetic) (2016) The non-symmetric Nitsche method for the parameter-free imposition of weak boundary and coupling conditions in immersed finite elements. Computer Methods in Applied Mechanics and Engineering, 309:625-652.
Yu Y, Perdikaris P, Karniadakis GE (2016) Fractional modeling of viscoelasticity in 3D cerebral arteries and aneurysms. Journal of Computational Physics, 323:219-42.
Perdikaris P, Insley JA, Grinberg L, Yu Y, Papka ME, Karniadakis GE (2016) Visualizing multiphysics, fluid-structure interaction phenomena in intracranial aneurysms. Parallel Computing, 55:9-16.
Xie F, Yu Y, Constantinides Y, Triantafyllou MS, Karniadakis GE (2015) U-shaped fairings suppress vortex-induced vibrations for cylinders in cross-flow. Journal of Fluid Mechanics, 782:300-32.
Yu Y, Xie F, Yan H, Constantinides Y, Oakley O, Karniadakis GE (2015) Suppression of vortex-induced vibrations by fairings: A numerical study. Journal of Fluids and Structures, 54:679-700.
Yu Y, Bittencourt ML, Karniadakis GE (2014) A semi‐local spectral/hp element solver for linear elasticity problems. International Journal for Numerical Methods in Engineering, 100(5):347-73.
Steinman DA, et al. (groups are ordered in alphabetic) (2013) Variability of computational fluid dynamics solutions for pressure and flow in a giant aneurysm: the ASME 2012 Summer Bioengineering Conference CFD Challenge. Journal of biomechanical engineering, 135(2):021016.
Yu Y, Baek H, Karniadakis GE (2013) Generalized fictitious methods for fluid–structure interactions: analysis and simulations. Journal of Computational Physics, 245:317-46.
Yu Y, Baek H, Bittencourt ML, Karniadakis GE (2012) Mixed spectral/hp element formulation for nonlinear elasticity. Computer Methods in Applied Mechanics and Engineering, 213:42-57.

Preprints

Yin N, Gao T, Yu Y, Ji Q, Ma T, Wei D, Efficient non-parametric DAG structure learning.
You H (Ph.D. student), Yu Y, Silling S, D'Elia M, Data-driven learning of nonlocal models: from high-fidelity simulations to constitutive laws.
Yu M, Sang Y, Pu K, Wei Z, Wang H, Li J, Yu Y, Zhou J, Few-shot character understanding in movies as an assessment to meta-learning of theory-of-mind. arXiv preprint arXiv:2211.04684.
Li B, Yu Y, Yang X The sparse-grid-based adaptive spectral Koopman method. arXiv preprint arXiv:2206.09955.
Liu N, Fan Y (Ph.D. student), Zeng X, Klöwer M, Yu Y, Harnessing the power of neural operators with automatically encoded conservation laws. arXiv preprint arXiv:2312.11176.
Lee D, Zhang L (Ph.D. student), Yu Y, Chen W, Deep neural operator enabled concurrent multitask design for multifunctional metamaterials under heterogeneous fields. arXiv preprint arXiv:2312.02403.
Silling S, Jafarzadeh S (Postdoc advisee), Yu Y, Peridynamic models for random media found by coarse graining.
Jafarzadeh S (Postdoc advisee), Silling S, Liu N, Zhang Z, Yu Y, Peridynamic Neural Operators: a data-driven nonlocal constitutive model for complex material responses.

Outreach Activities

One Nonlocal World Project

The One Nonlocal World Project is an online platform where people working on nonlocal problems or interested in learning more about this topic can regularly check for updates on nonlocal modeling, analysis and computation. The short-term goal is to keep researchers connected virtually by online workshops and schools during these unconventional COVID times. The long-term goal is to build up new communication channels for a more connected and inclusive research community on nonlocal models

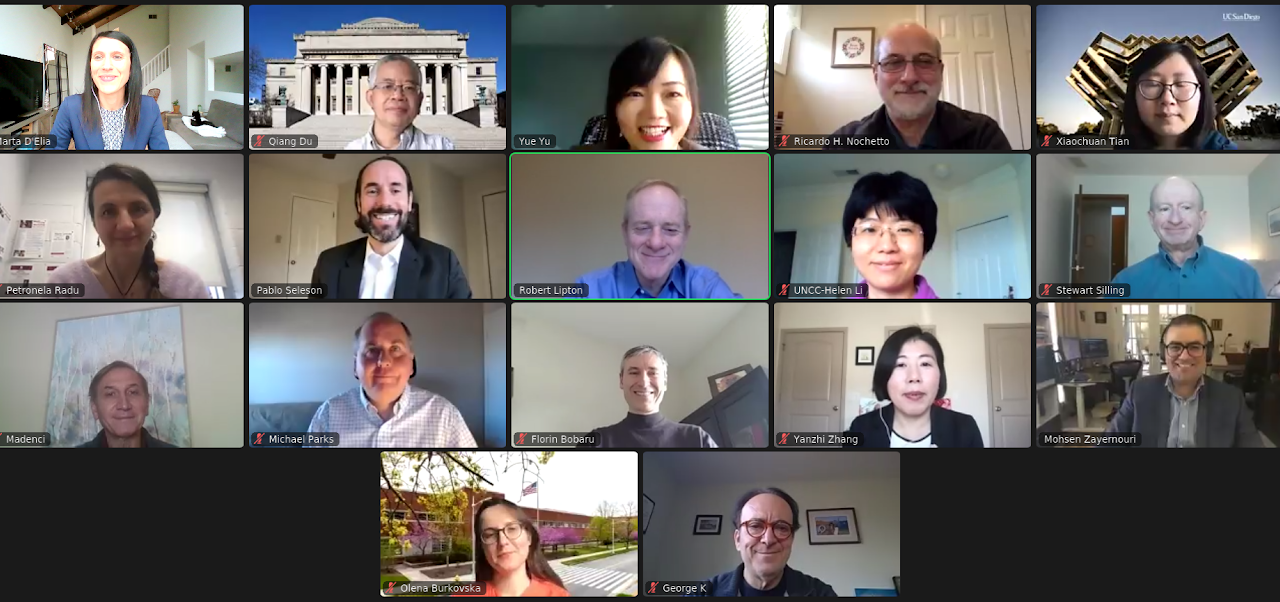
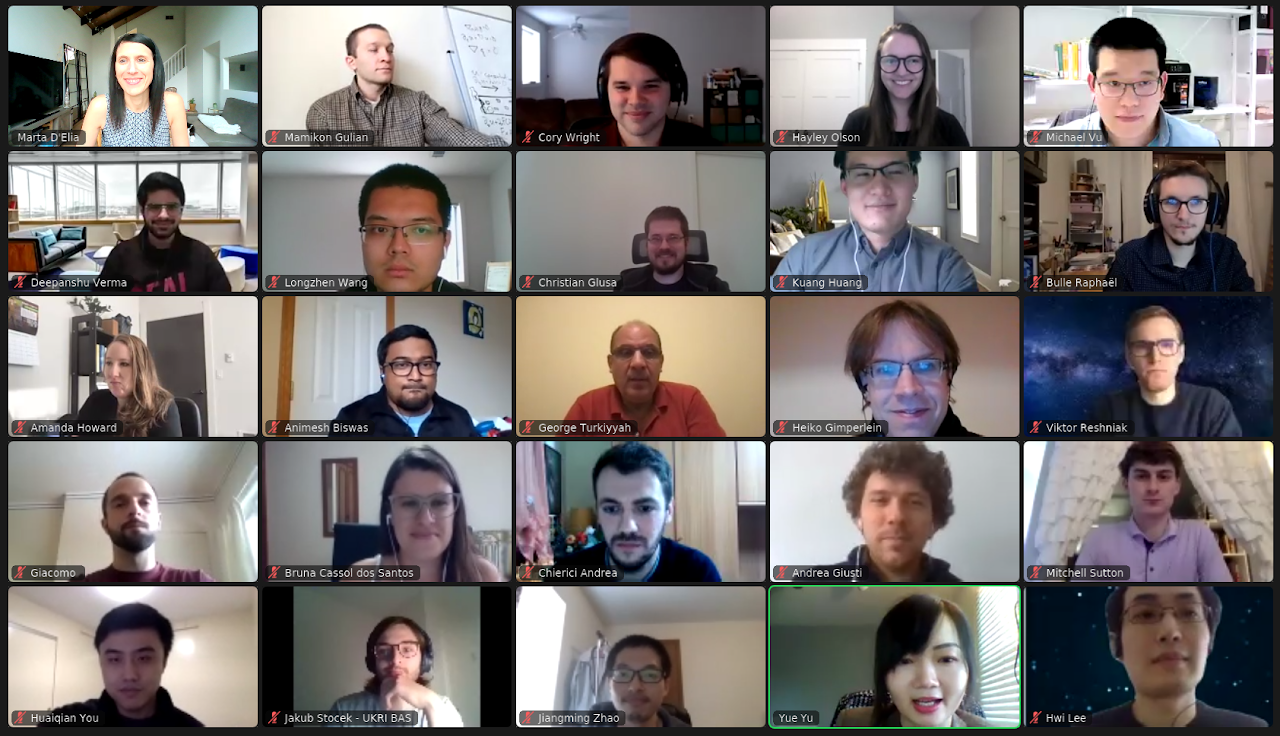
Pictures from the 2021 One Nonlocal World Opening Event.

Dr. Marta D'Elia, Dr. Qiang Du, Dr. Petronela Radu, Dr. Pablo Seleson, Dr. Xiaochuan Tian and Dr. Yu founded the nonlocal world project and organize activities regularly.

The 2021 opening event took place on 22 Jan.-23 Jan, 2021, with video records available on the One Nonlocal World YouTube Channel. Please register on the One Nonlocal World website for announcements of future events. To announce new events and activities on the platform or through our email list, please contact Dr. Marta D'Elia and Dr. Yue Yu.

The Annual High-Performance Computing Workshop

The HPC workshop is a high-performance computing (HPC) workshop sponsored by the National Science Foundation, the Lehigh ADVANCE program, and the Department of Mathematics, for students, faculty members from the Lehigh Valley Association of Independent Colleges (LVAIC) schools and the general public in Lehigh Valley area. The workshop aims to promote female researchers in scientific computing therefore would prefer female attendees, but male attendees are also welcome. Besides tutorials and hands-on exercises, researchers working on high-performance computing in both academic and industry will also present in the workshop, so the attendees will have opportunities to get connected with these researchers.

Poster and pictures from the 2017 HPC workshop.

Dr. Yu and Dr. Pacheco host the workshop annually, typically near the end of the spring semester. Further details will be posted during the spring semester.

SIAM New York-New Jersey-Pennsylvania Section

The SIAM NNP Section is a regional subgroup of the Society for Industrial and Applied Mathematics (SIAM) members. The section was found in 2022. It aims to enhance communication among its members, to promote collaboration for both basic research and applications of mathematics to industry and science, and to support the SIAM mission in the great states of New York, New Jersey, and Pennsylvania.

Pictures from the first SIAM NNP annual meeting at NJIT. Left: the President of SIAM NNP, Prof. Roy Goodman, is giving the opening remarks. Right: Prof. Silvia Bolaños, Prof. Kathleen Kavanagh, and Prof. Yue Yu are organizing the student events.

The second SIAM NNP annual meeting will take place at the Rochester Institute of Technology in 2024. Further details will be posted during the spring semester.