Topologies

Mark H. Bickhard
Department of Psychology
17 Memorial Drive East
Lehigh University
Bethlehem, PA 18015
mhb0@lehigh.edu
http://www.lehigh.edu/~mhb0/mhb0.html

Robert L. Campbell
Department of Psychology
Brackett Hall 410A
Clemson University
Clemson, SC 29634-1511
robert_campbell@quickmail.clemson.edu

Deepest thanks are due to the Henry R. Luce Foundation for support to Mark Bickhard during the preparation of this paper.

We will first outline some architectural requirements for models of learning and development, then present a model of representation that poses its own architectural requirements. The requirements for representation, it turns out, will also satisfy the requirements for learning and development.

A major architectural requirement imposes itself on any system that can profit from past successes and failures -- in other words, any system that can learn and get better at learning. That requirement is a functional topology in the space of possible constructive products of learning and development. The basic intuition is that, if previous problem-solving successes are to be functionally useful in attempts at solving new problems, there must be some way to "locate" and make use of the old problem representations and solutions that are "closest" to the new problem representations, or at least "nearby." Such closeness information constitutes a topology. Exploration of these topological requirements yields strong constraints on the nature and locus of learning and of development.

Such topological considerations are not well addressed within standard architectural and mathematical approaches to computation. In finite state machines, Turing machines, or programming languages, topologies do not naturally arise. When Artificial Intelligence researchers encounter the constraints that yield the necessity for such topologies, the standard fix, as we shall discuss below, is to introduce feature-based topologies. In these topologies, things are "nearby" if they share many features. Feature-based topologies turn out to be intrinsically inadequate for a number of reasons. We will find, in fact, that the need for adequate topologies forces us to consider an architecture that is quite different from standard computational frameworks. Our proposal also happens to be much closer to aspects of the functional architecture of the central nervous system. If our analyses are correct, it is no accident of implementation that the brain functions with fields of oscillations engaged in mutual modulations.

* Learning and development must be constructive because knowledge is constituted as functional system organization, and system organization cannot be transduced or induced from the environment.

* The constructions must proceed by variation and selection because errors of construction are inevitable, and system constructions can at best search in the space of functional selection pressures.

* The constructive process must be blind because otherwise it would already know what is to be learned or developed, and such knowledge is precisely what must be accounted for. Some sort of evolutionary epistemology is required to account for learning and development (Bickhard, 1988, 1992a; D. Campbell, 1974; Hooker, 1995; Radnitzky & Bartley, 1987).

Beyond the limiting case, however, learning is usually not blind. It does involve prior knowledge, at least in a heuristic form -- knowledge of sorts of problems associated with sorts of likely solutions. Such prior knowledge, of course, is the product of earlier constructions, whether developmental or evolutionary, and its ultimate ground must also be blind processes (Bickhard, 1992a). The focus of our discussion will not be on the ultimate origins of heuristic knowledge, however. Our concern will be how such heuristic knowledge, based on prior learning and problem solving, could be functionally constituted in and for the knowing system. We will seek to identify some functional and architectural requirements for the existence of heuristic knowledge.

Before we can begin the primary explorations, however, certain preliminaries must be established. Our considerations about learning build on a model of the nature of representation, called interactivism, and its attendant constraints on the nature of learning. From the interactivist standpoint, learning and development must involve constructive processes operating by variation and selection. And there are two more exotic constraints: 1) A cognitive architecture of oscillatory processes that modulate one another is required -- a conception that converges in striking ways with contemporary studies of the functioning of the central nervous system. And 2) there must be a process of microgenesis to shift among modes of functioning.

Our argument proceeds as follows:

1) Representational phenomena require an interactive treatment of representation.

2) The interactive conception, in turn, requires an architecture of (neural) oscillations and modulations, and processes of microgenetic construction.

The first two points actually serve to introduce and motivate our main topic -- the need for constructive topologies in models of cognition, and the form that a model of constructive topologies might take:

3) We show that heuristic learning and development require functional topologies, as well as the ability to construct new topologies.

4) Finally, we show how such topologies naturally arise in a cognitive architecture of modulated oscillations that includes microgenetic constructive processes.

We have to consider the possibility that the activity of detecting the fly and the activity of initiating the tongue flick are one and the same. Even if this were the case, however, it might be possible to distinguish two different epistemic functions served by the same neural processes. We need to recognize that the flow of process in the frog from fly detection to actual tongue flick is not a direct causal flow or an impenetrable reflex arc. If a shadow of a predatory bird appears for the frog just as it is about to flick its tongue, the frog will most likely jump into the water to avoid being eaten itself, rather than proceed with the tongue flick. In other words, the connection between fly detection and tongue flicking must be some sort of indication of possibility, a possibility that may be pursued depending on other circumstances. Fly detection does not merely trigger tongue flicking in some ballistic fashion.

Standard usage would describe the fly detection processes as constituting a representation of the fly for the frog. The frog then uses that representation to "infer" the possibility of flicking its tongue and eating. The causal processes that encompass the light reflecting from the fly, entering the frog's eyes, and stimulating the ensuing neural activities are presumed to endow these neural processes with the status of representations and bestow representational content on them. The representational content, and, thus, the very representationality of these activities in the frog are supposed to follow from their having been caused by the fly. Representation is taken to be this causal correspondence -- or at least the causal correspondence is viewed as its essential core (Dretske, 1981, 1988; Fodor, 1987, 1990; Hanson, 1990; McClelland & Rumelhart, 1986; Newell, 1980a, 1990; Rumelhart & McClelland, 1986; Smith, 1987).

There is at least one different option, however. Maybe the representational content of the frog's neural activities upon the detection of a fly is an indication that tongue flicking and eating can now be done, rather than a representation of the fly as such. In this view, the representational content is about the potentialities that the environment affords for the frog's further actions and interactions -- the interactive affordances of that environment (Bickhard & Richie, 1983; Gibson, 1977). It is not about the present or immediately past actualities in that environment -- even if detecting those immediately past actualities is what sets up those indications of potentialities.

In the standard conception, the frog infers the possibility of tongue flicking from a representation of a fly. In principle, at least, the standard approach encompasses both the supposed representation of something actual -- the fly -- and something potential -- the inferred possibility of tongue flicking. But indications of potentiality are never, in standard approaches, taken to be a fundamental form of representation. They can qualify as representational only in an indirect and derivative sense, because the representation is fundamentally constituted as correspondence with what is being represented. Most commonly, they are not thought to be representational at all; they are reduced to purely causal or functional phenomena of initiating, guiding, and controlling action.

In any case, there are two candidates for representational content: the fly, on correspondence grounds, and the possibility of tongue flicking and eating, on the basis of indications about potentialities that are offered by the environment. We could reject both, accept both, accept only correspondence, or accept only indications of potentiality. Those who insist on reflexive consciousness before they will credit the system with representation might want to reject both -- at least in the frog's case. (It is not so clear how the advocates of mandatory reflexivity would accommodate the case of a baseball player seeing a fly ball and indicating, initiating, tracking, guiding, and controlling the catching of that ball.) One might even try to accept both, but these are two fundamentally different notions of the nature of representational content, and it is not clear how they could be integrated: in any case, we do not know of any attempts to do so. This leaves us with a choice between correspondence and indication of interactive possibilities.

The standard assumption is overwhelmingly that representation must be some form of correspondence, some sort of encoding. Its proponents often proceed as though there were nothing problematic about it (Vera & Simon, 1993a). Continued acceptance, however, comes in the face of extremely difficult and commonly acknowledged problems that have become the focus of much work in philosophy of mind (Dretske, 1981, 1988; Fodor, 1987, 1990; Hanson, 1990; Smith, 1987).[1] We will argue that the severity of these problems has, if anything, been underestimated -- representation as correspondence is a logically incoherent position. The acknowledged problems with this approach are insoluble, because they are symptoms of this deeper incoherence. We will argue for the alternative position that representation must be understood in terms of indications of interactive potentialities.

There are many objections against representation as correspondence, each of which comes complete with counter-arguments and counters to the counters. We will present two of the arguments in abbreviated form.

The incoherence argument. The first argument derives from considering a simple question. How does the system know what is on the other end of supposed representational correspondences? How, for instance, could the frog's activities that constitute a factual detection of a fly also constitute a representation for the frog with a fly as its content?

We have to insist on the proviso "for the frog" because any neuroscientist, psychologist, or other observer, could notice that such-and-such neural activity in the frog is stimulated by flies. The observer could construct a correspondence relation between two things that the observer knows: the neural activity in the frog and the presence of a fly. Such a move may be useful for the observer, but it cannot help the frog. The frog does not have the observer's independent epistemic access to its own neural activities, on the one hand, nor to flies in its environment, on the other hand, so it cannot draw any epistemic correspondence between the one and the other. If there is any representation of the fly for the frog it must be constituted in the very activity of fly-detection.

The problem is not how the frog could detect the fly. That is no more difficult in principle than a photocell opening a door, although the pattern detection process may be considerably more complicated. The problem is rather that detecting the fly and initiating consequent further activity form a strictly functional set of relationships, and do not require that those detections constitute representations. The detection process does not even require that any information be available to the system about what has been detected. All that has to happen for the frog is that fly detection and eating work well enough for individual frogs, and more generally the species, to survive and reproduce. Survival and reproduction, in turn, require that those detections be often enough of flies (or worms, or something nourishing) in fact, but not that frogs have any representations of flies as such. All that is required here is a functional account, not an epistemic account. Not all phenomena involved in perception and action need be or can be representational (Greeno & Moore, 1993).

As soon as this functional account is made out to be an epistemic account, a problem arises. How could the frog have any internal functional information about what its fly detections have detected? We presume, by contrast, that the frog could have internal functional information about what to do with such detections, i.e., tongue-flicking and eating (for an approach to functional modeling which addresses some of the internal problematics at the functional level of analysis, see Bickhard, 1993). Detection can generate factual information, in the sense of generating factual correspondences and covariations with what has been detected. But how could such relationships of correspondence or covariation constitute representations (Hanson, 1990)?

We contend that the problem is insoluble. Detection activities (or products), in the standard epistemic story, are supposed to constitute representations of what they have detected, yet representational information about what is on the other end of the correspondence is precisely what is at issue. In effect, correspondence is supposed to provide representational content. Each correspondence is supposed to specify what it is a correspondence with. But correspondence is a factual relationship, not an epistemic relationship. Correspondences are everywhere -- every single instance of every single lawful regularity in the universe is a factual correspondence -- but representation is not. To be in correspondence with X is not to represent X. Any representation of X, or representation of any correspondence with X, must come from somewhere outside of that correspondence. Neither factual correspondence relations nor the elements that participate in them constitute representations. They do not represent the correspondence relations themselves; they do not represent the elements on the other end of such relations.

The jump from factual correspondences to representations, then, presupposes that factual correspondences can provide representational content, yet they must already have representational content to qualify as representational correspondences in the first place. The jump from factual correspondences to epistemic correspondences presupposes the very representational content it was supposed to account for. Such a move is circular, and therefore incoherent: it requires that X, the representational content, already exist in order to account for the existence of X.

One corollary of this incoherence argument derives from noting that paradigm "representations" are all external: they are pictures, statues, blueprints, ciphers, written texts, and so on. External representations must be interpreted by some epistemic agent or they do not function as representations. Such interpretive usage is one of the phenomena to be understood. When discussing internal representation, however, investigators widely assume that it has the same ontological character as external representation. One merely codes externally while the other codes internally. The trouble is that internal representation CANNOT be the same as external representation.

External representation requires interpretation. Internal representation, on the other hand, is a constitutive property of an interpretive agent -- not merely an external resource for an interpretive agent -- so any account of internal representation must be able to account for the agent itself. If we equate internal representation with external representation, we end up with an infinite regress of homunculi -- an endless series of mini-agents, each of which has to interpret the results of the preceding agent's interpretation.[2] Equating internal with external representation slides back into logical incoherence: interpretive representational content must already be there in order to account for interpretive representational content. Internal and external representation are different kinds of things; treating them as the same kind of thing is a category error (Clancey, 1993; Slezak, 1992, 1994).[3]

There are many elaborations, corollaries, counters, and counters to the counters, for this argument -- so, needless to say, our presentation is far from complete. Indeed, the many problems involved in attempting to understand representation as correspondence are extensively addressed in the literature, though it is still assumed that the correspondence approach will emerge victorious in the end (Fodor, 1975, 1987, 1990; Fodor & Pylyshyn, 1981; Hanson, 1990; Harnad, 1989; Loewer & Rey, 1991; Newell, 1980a, 1990; Palmer, 1978; Pylyshyn, 1984; Smith, 1987; Vera & Simon, 1993a).

In most of our previous work, we developed this same network of argumentation against correspondence notions of representation as a critique of encoding-based conceptions. Encodings, roughly speaking, are representations constituted by virtue of correspondences with what is represented (Bickhard, 1987, 1992a, 1993, in preparation-a; Bickhard & Campbell, 1992; Bickhard & Richie, 1983; Bickhard & Terveen, 1995; Campbell & Bickhard, 1986, 1991, 1992a, 1992b). The error does not lie in recognizing the existence of encodings such as pictures, statues, blueprints, Morse code, and ASCII codes. The error lies in the assumption that mental representation can be the same kind of thing as such external encoded representations. Mental representation cannot require an epistemic interpreter.

What we have presented is sufficient, we hope, to indicate the profoundly serious questions in principle about encodingism, or representation as correspondence. Our second argument extends these criticisms and goes on to explore the other possibility: representational content as indications of potential further interactions. It has the additional virtue of introducing questions of learning.

The learning argument. The learning argument is complex (Bickhard & Terveen, 1995). The basic intuition of the argument is that learning requires error, and, because what we call interactive representation is the only model of system representation that can account for representational error, it is the only model of representation that can account for learning.

We have divided the argument into two parts, each with several steps. The first part of the argument is, roughly, that learning requires system-detectable error and system-detectable error requires system interaction. The second part contends that only interactive representation could be in error for the system, so only interactive representation can be learned.

The first part of our argument breaks into three steps: 1) learning requires internal change, 2) adaptive or appropriate internal change requires error, and 3) error requires output. The second part of the argument takes the need to have output in order to be able to have error -- and to be able to learn -- and proceeds with the question of what could be in error. We argue that the output that induces an error -- or the internal organization that produced that output -- is what is in error. The error is an error of emitting that output under those conditions (whatever they are). But, if those relationships between internal conditions and outputs are what can be in error -- and, therefore, possibly not in error -- then it is those internal relationships that carry truth values. That is, it is those relationships among internal processes, whether actual or potential, that constitute representation.

In more detail, the first part of the argument shows that systems with no output cannot be learning systems. Step 1: It may seem obvious that learning requires some sort of change in the internal potentialities of a system, but there are ways of (mis)conceiving the problem in which that is not so obvious, so we offer an argument. Step 2: We argue that such internal change is appropriate only when an error has been made. To change a system under conditions of success is to risk undoing whatever was involved in that success, and to make changes without any information about what might need changing, or even what could be improved. Step 3: We argue that error requires output. If error could be generated and determined strictly internal to the system, then no learning would be required.

Learning requires change. In purely passive conception of representation as correspondence, it might appear that learning could occur without any internal system process. Impressing forms from out in the world onto an internal waxed slate (Aristotle, 1941; Locke, 1961) does not seem to require internally originated change. Appearances, however, can be misleading.

If we ignored the problem of acquiring representational content about what made the impression, we might think impression onto a waxed slate was plausible -- though only if the system's representations were confined to exact correspondences with whatever particulars impressed themselves upon it at particular times. But if representation is to have any generality, if representation is to categorize inputs and input patterns, then passive impression cannot be its origin. A given input or input pattern must be categorized in some way that goes beyond the details of the particular inputs, so its impression into the system cannot be simple causal imprinting onto a waxed slate. For example, a single visual picture of a particular chair cannot suffice as a representation of "chair" (Fodor, Bever, & Garrett, 1974).

These considerations reinforce our earlier point that whatever factual correspondences might be created by impressions in a waxed slate do not constitute or provide representations of what is on the other end. The neural activities that constitute a fly detection for a frog -- that have been "impressed" into the frog by that fly, or by the light therefrom -- do not thereby constitute a representation of a fly for that frog.

The need for categorization implies that the system must in some sense be prepared for the categorizations that it is capable of, via some sort of internal system process that goes beyond mere causal impressions. It must categorize this way rather than that way. Learning, in turn, involves the creation of new preparations, new capabilities for categorization, and that creation requires change of some sort within the system.

Adaptive change requires error. Learning requires change, but change is only appropriate under conditions of error.[4] It makes no sense to prepare for new possible categorizations when the current potential input-pattern categorizations are working just fine. Change without appropriate (error) triggering risks undoing perfectly adequate system organizations. So, we conclude that learning requires not only change but also error.

System-detectable error. Such error must trigger change in the system, so information about error must be functionally available within the system. Error must be error for the system, not just from the perspective of someone observing the system.[5] And because functionally efficacious error must be error for the system itself, two consequent issues arise: 1) How could error be detected by a system? 2) What could the system take to be in error? (What could be altered by the system in attempting to remove or avoid the error?) The first issue leads to the need for output, and concludes the first portion of the overall argument; the second issue introduces the second portion of the argument, focusing on the nature of representation.

What could error be? The conclusion that we reach in this section of the argument is that, in general, error requires outputs to some environment with subsequent inputs to the system. It is those outputs, emitted in whatever internal system conditions obtained at the time, that can be in error, and it is the unexpectedness of the subsequent inputs that constitutes error for the system.

Issues about the nature of error and about system requirements for error are complicated, however, by the existence of error indications that have been designed into the system or built into it by evolution, such as pain signals. Built-in error signals tempt us to conclude that error is whatever yields such an error signal. Special-purpose error signals, like pain, can be designed in; they can also arise through evolution. But not all error signals can be built in, because not all learning depends on external reward or punishment.

Let us start with strictly passive systems -- systems with no outputs. A system with no outputs can do nothing but process and categorize inputs or input patterns. In such a passive architecture, there is nothing to differentiate two fundamentally different kinds of inputs: those that constitute or signal error, and those that simply need processing. Error inputs cannot be differentiated from "ordinary" inputs because there is no contingency between processes in the system and purported error inputs. There is no connection between system activities and "error" inputs that would enable any system activities or outcomes to be taken to be in error. In a passive system, all inputs are simply more inputs to be processed. (If, on the contrary, we suppose that no error feedback is required at all, then the system is already capable, on a strictly internal basis, of determining whether the results of its input processing are correct or in error. If no error feedback is required, then no learning is required.)[6] It makes no difference whether the input processing is of an information-processing or a connectionist sort. Passive systems -- systems with no output -- cannot make errors. Consequently, passive systems cannot learn (Bickhard & Terveen, 1995).

Built-in error signals might suggest a specious counterexample to this argument. Couldn't a passive system have pain inputs, and wouldn't those signal error? Wouldn't pain signals provide error information even for passive systems? Dedicated error signaling certainly occurs. But in a strictly passive, outputless system -- even if there were something like pain inputs -- what could bring about pain inputs or other error signals? What could ever evoke them? What, in fact, could a passive system do that would be in error?

In general, the system must do something in order to be in error, and something outside the (sub)system must indicate that it is in error. Error detection and signaling processes cannot, in the general case, happen only inside the system. For such processes to be strictly internal, the system would already have to have information about what is in error and what is not. And if the system already had this information, it wouldn't need to learn at all -- it could just keep processing until it got an acceptable answer. Either a system already anticipates the correct result, in which case it does not need to learn, or the system doesn't anticipate it and must output its activities, or the results of its activities, to some other process that can generate error feedback. That is, learning requires output and error feedback.

Up to this point, we have argued that error requires output and error feedback, but we have been restricted to built-in forms of feedback. In the general case, built-in error signals are not logically required, however useful they might be for some purposes.

What could be in error? Error determination and error signaling must arise from outside the system, and, therefore, in response to some output from the system. A system with no output cannot receive error signals, and, therefore, cannot learn.[7] The crucial question at this point, then, is what could be taken to be in error. Our answer is that if only output can, via the environment, initiate error signals, then it is only output that can be taken to be in error. Classifications of the input, in such a view, are in error only insofar as they yield erroneous outputs, or erroneous indications that some output could or would be appropriate. So the fundamental attributions to the environment that can be found to be in error by the system are attributions that various outputs would be appropriate or possible, and that those outputs would have particular input consequences. This latter condition is crucial, because it is only via consequences for further inputs that the system can have internal functional access to any consequences of its outputs.[8]

Error without specialized error signals. This last point allows us to generalize beyond pain and other dedicated error signals to a broader conception of error-constituting inputs. In a learning system, functional connections between input processing and outputs are stable only insofar as they do not yield error signals; there is a functional sense in which the system is not "expecting" error signals if it does produce some particular output. Without triggering learning processes, the system is functionally prepared to process any consequent inputs it expects to receive. Expected inputs are those that the system is already functionally organized to handle. What makes pain signals function as error signals is that they cannot be processed within the basic system organization without invoking learning processes (that is, processes that change that system organization).

None of this requires the error signals to be predesignated as such. All that is required is that the system be functionally unprepared to process some subsequent input, given that it has just engaged in some process of interacting and emitting outputs -- that an encounter with such functional unpreparedness be sufficient to trigger learning. In an automaton, for example, an undefined condition or an infinite loop might suffice to indicate error and to trigger learning processes -- without any particular input type being specially designated as an error input.

Error, then, can take the form of inputs for which the system is functionally unprepared -- inputs that the system is not[9] set up to handle at the moment. The general notion allows any input to be functionally "unexpected" under some system conditions.[10]

Interactive representation: what can be in error. We can now draw these general conclusions. (1) It is only connections between output and subsequent input that the system is not prepared for, or, more generally, flows of system-environment interaction that the system is not prepared for, that can be taken to be in error by that system. (2) If such functional expectations of possible future interactions (or flows of interaction) are all that can be found to be in error for a system, then they are, conversely, all that can be found not to be in error. Only such interaction expectations, or indications, can be retained by the learning system when they are not found to yield error. Thus (3) it is only such indications of interactive potentiality that can constitute representations for the system -- assuming that representations must at least be potentially falsifiable by the system and for the system.

Implicit Predication. Indications of interactive potentiality are not just pragmatic indications of what is possible for the system. They are also, at least implicitly, predications about the environment. They predicate of the environment, implicitly, whatever those interactive properties are that could support the indicated interaction by the system with that environment. As implicit predications about the environment, such indications of interactive potentiality have the logical form we would like in order to be able to model representation for the system. They have:

* a logical subject -- the current environment;

* a logical predicate -- the interactive properties;

* and the possibility of being false, of having a truth value, from the system's own functional perspective.

Although indications of interactive potentiality have truth conditions, they do not represent those truth conditions. They have truth conditions because they can yield failure unless the current environment supports the output-to-input side of the interactive indications; they are false if their implicit predications about the environment are false. They do not represent those truth conditions,[11] because there is no information internal to the system that identifies those required environmental conditions. The system can, fallibly, detect instances in which those indications are false, but it has no direct information about the truth conditions that have been falsified.

Learning, then, requires error, and error requires anticipations of the flow of interaction. Only anticipations of the flow of interaction can be found by the system itself to be in error, and, therefore, only such anticipations can be bearers of truth values for the system. Only such interactive anticipations can be representational for the system.

In this argument, we have taken the need to account for learning as pivotal. Error arises as a requirement for learning; interactive representation arises as the sort of thing that could be learned. There is a related two part argument that pivots on error per se rather than on learning (Bickhard, 1993, in preparation-a). The first part of this related argument points out that representation must be capable of being in error for the system itself. Only if representational error is system-detectable can representation be naturalized. Only with system-detectable error are error-guided activities, such as goal-directedness and learning, possible. The second part of this argument is that the only thing that can be in error for the system itself is internal anticipations of the internal consequences of system interactions -- and it is those anticipations (properly rendered in strictly functional terms) that we identify as interactive representations. The argument that we have given and this alternative version converge on the final point: because representational learning requires system-detectable representational error, only interactive representations can be learned.

Either version would suffice, but we are aiming toward issues of learning, and so have presented the version of the overall argument that focuses on what is required for learning.[12]

Interactive representation. Both of our arguments -- the incoherence argument and the learning argument -- imply that representations cannot be defined in terms of input correspondences. The learning argument directly supports a positive alternative: representational content is constituted as the indication of possibilities for interaction. For our frog, then, what is most fundamentally represented is not flies; rather, it is potentialities for tongue flicking and eating.

For a slightly more formal perspective on interactive representation, consider a system in interaction with an environment. The internal course of processes in such a system will depend in part on the functional organization of the system, and in part on the environment that is being interacted with. Similarly, the internal state that the system ends up in when the interaction is completed will depend, in general, on the environment interacted with. Some environments will yield that final internal state in interaction with this system, and some environments will yield other final internal states. Each possible such final state, then, implicitly defines the class of environments that will yield it, and, in interaction, differentiates instances of that implicitly defined class of environments from those of other such classes of environments.[13]

A passive input processor could make such differentiations -- the simplest case is sensory "transduction." Usually, however, differentiations, or implicit definitions, of environments are taken to constitute representations of what has been differentiated; transduction is thought to produce "sensory codings." Passive input processors are taken to yield encoded representations of what has been differentiated, of what is on the other end of the correspondence. The interactive model, in contrast, does not ascribe any explicit representational content to such differentiations, thereby avoiding the customary logical incoherence and category errors.

From our standpoint, those differentiating internal final states can serve to select further system interaction. Having differentiated one kind of environment (the kind that yields internal final state A, say), the system may proceed in a different fashion than if it had differentiated a different kind of environment (for instance, the kind that yields internal final state B).

So, having differentiated the kind of environment that happens to correspond to a fly, the frog may then differentiate its own further activity into a tongue-flicking-and-eating mode. This does not require that the frog have any representational content about flies, but it does mean that the frog has representational content about this environment: it is a tongue-flicking-and-eating type of environment. That content, in turn, can be in error, and the frog, in turn, is capable of discovering it to be in error. This is error for the system, error detectable as such by the system.

There are many more questions that the interactive conception must deal with. Even though we have predications, with truth values that can be tested by the system (defeasibly, of course), interactive representations do not look much like our familiar world of objects in space and time, connected by causal relations, and so on. Interactivism might do for frogs, but what about human beings? We cannot elaborate an answer in this paper, but we can indicate how such an answer is possible.

From the interactivist standpoint, the primitive form of object representation is of potentially quite complex organizations of possible interactions and of dependencies among those interactions. These organizations, if they are to represent objects, have one key additional property: they are invariant under many other classes of interactions that the system might engage in. There are two parts to this suggestion: the complex organizations of indications, and the invariances.

Individual indications will have the form, for example, of "If this interaction is engaged in and arrives at that internal condition, then this other interaction could be engaged in and would arrive at those other internal conditions." Complex systems will have complex webs of such indications, with the resultant internal conditions of some indications constituting the indicating conditions for others -- often in interlocking and circular organizations of indications of potentialities. Organizations of complex dependencies among possible interactions are intended to capture, for example, the fact that an object offers many possibilities for interaction: it can be visually scanned, slid, rotated, thrown, sat on, crawled around, and so on. All of these are retrievable as possibilities, under many conditions, even if they cannot be done proximately and immediately. So, if I turn this book over, the visual scans that were possible a moment ago are not currently available, but if I turn it back over, then those same visual scans become possible again. The overall organization of possibilities includes many relationships between possible interactions and other interactions on which their possibility depends. In this view, a book is represented as an organization of dependencies among interactive possibilities.

That overall organization remains unchanged under many many things we can do. We can move the book, store it, lend it (usually), open it, flip through the pages, and so on, and still return to any particular set of proximate interactive possibilities -- the organization of such possibilities is invariant under all such intermediate interactions. On the other hand, if we incinerate the book or dissolve it in sulfuric acid, then that organization is destroyed -- the interactive potentialities and dependencies among those potentialities no longer exist. From an epistemological perspective, it is precisely such invariances of organizations of interactive potentiality dependencies that constitute objects.

Ours is a generally Piagetian notion of object representation, and the inspiration for our models of representation for objects in space and time, causal relationships, and so on, is similarly Piagetian (e.g., Piaget, 1954). We suggest that our familiar world is constructed out of predications of interactive potentiality, or, in a generally Piagetian sense, that representation is emergent out of action.

More broadly, the interactivist framework can be seen as a generalization of pragmatist notions of representation (Houser & Kloesel, 1992; Murphy, 1990; Rosenthal, 1983, 1987, 1990; Thayer, 1973). Pragmatists rejected the "spectator" conception of knowledge, the view that knowledge could be available to passive systems that merely process inputs. Instead, they regarded internal anticipations of interaction with an environment as representational. This basic affinity holds despite some important disagreements between interactivism and classical pragmatism.

Many additional questions ought to be asked about the adequacy of the model of representation that we have proposed, but our purpose here was simply to make a prima facie case. More complete presentations can be found in Bickhard (1980, 1992a, 1993, in preparation-a, in preparation-b), Bickhard and Richie (1983), Bickhard and Terveen (1995), and Campbell and Bickhard (1986). Having established the reasonableness of an approach to representation in terms of interaction, rather than correspondence, we now consider the consequences of such a conception of representation for the nature of learning.

Interactive learning. The implications for learning, at least those we need at present, are fairly straightforward. If representation consists of correspondences with what is being represented, then it is tempting to think that such representational correspondences could be created by impressions from the world into a passive mind. The empiricist's waxed slate is the paradigm; its modern variants are technologically more sophisticated, but the underlying assumptions have not changed.[14]

Things turn out differently if representation is emergent from action, specifically as dependency organizations of indications of potential interaction. There is no longer any temptation to think that such organizations could be impressed by the world into a passive mind. Interactive representation is not constituted as structural correspondences with what is represented, but, rather, as interactively competent functional system organization. Such system organization must be constructed -- it cannot be impressed. Consequently, the interactive model of representation logically forces a constructivist conception of learning and development.

Such a constructive process cannot be assured of engaging in the right construction for any arbitrary set of new circumstances. If the system had constructive processes that could make the correct constructions on first encounter with new circumstances, it would know the correct constructions in advance. But knowledge of what to construct -- and the origins of such knowledge -- are precisely what is at issue for learning and development. Foreknowledge of what will work cannot always be available.

Indeed, foreknowledge cannot be logically required for the construction of new knowledge, on pain of infinite regress. Requiring that knowledge already exist in order for knowledge to be created generates such a regress (Bickhard, 1991b). Correspondence-based models of representation, for example, cannot account for the creation of new encodings. They can account for new instances of already available encodings, or new combinations of already available encodings (e.g., Brachman, 1979), but not new foundational atomic encodings. Foundational encodings require a specification of what is on the other end of the encoding, but that representational content is precisely what the encoding is supposed to provide. The representational content is required in order to get the encoding, and the encoding is required in order to get the representational content. This yields an infinite regress: the system must already have representational content in order to get it.

Some have sought to escape from this trap by claiming that no new foundational encodings are learned or developed -- they are all innate (Fodor, 1975, 1981). But the foundational encoding trap is a logical impossibility, not a problem of implementation. Adversions to innate knowledge, and consequently to its sources in evolution, are totally irrelevant (Bickhard, 1988, 1991a, 1991b; Campbell & Bickhard, 1987). If it can't be done, evolution can't do it either: "the argument has to be wrong, ... a nativism pushed to that point becomes unsupportable, ... something important must have been left aside. What I think it shows is really not so much an a priori argument for nativism as that there must be some notion of learning that is so incredibly different from the one we have imagined that we don't even know what it would be like as things now stand." (Fodor in Piattelli-Palmarini, 1980, p. 269)

The consequence, we argue, is unmistakable: representation is interactive, so learning and development must be constructive. Constructions cannot require foreknowledge of what to construct. In the limit, they must be blind. They must involve trial and error, variation and selection, as the minimal-information process for attempting to achieve success or fit or correctness for the constructions and their implicit environmental predications. In short, learning and development cannot be understood without adopting an evolutionary epistemology (Bickhard & D. Campbell, in preparation; D. Campbell, 1974; Hooker, 1995).

Naturally, a great deal of learning and development do make use of foreknowledge. We have not denied its existence, just argued that it cannot be required to exist. Our major task in this article, in fact, is to explain precisely how such foreknowledge could exist and could guide new constructions by a system. Accounting for constructive foreknowledge turns out to require a new architectural property, one that cannot be found except in the most rudimentary forms whether we seek it in artificial intelligence, cognitive science, cognitive psychology, developmental psychology, or linguistics. The architectural property we need is functional topologies in representational and system spaces.

We begin with arguments for an architecture of modulated oscillations. The key points are that interaction requires timing, and that single clocks driving an entire system (as is done in standard computers) do not make a plausible architecture in which timing could be realized in evolved systems. An architecture of oscillations and modulations can address such timing considerations, and is evolutionarily plausible.

In classical correspondence conceptions, representation is constituted as logically atemporal correspondences between representational elements and what is represented. There may be temporal processing of the representational elements, because what needs representing keeps changing, and because inferences need to be carried out. But the representations per se do not intrinsically involve timing.

Timing. For a model that treats representation as emergent out of interactively competent system organization, however, timing is of the essence. Most kinds of interactions can fail for timing reasons, as well as for organization or patterning reasons. And timing failures can involve being either too fast or too slow -- the issue really is timing and not just speed. Catching a ball, walking, driving a car, all require careful timing to succeed. Indeed, if objects are epistemologically constituted as invariances of patterns of interactive possibilities, then our knowledge of objects (and the rest of our familiar world) involves timing issues. Timing is at the heart of representation and knowledge. Representations in general cannot have representational content without timing.

Now the classic computer metaphor certainly involves time -- the search for faster computers is intense and productive. But nothing in the encoded symbols that are taken for representations in such models requires time. After all, content for the symbols is provided by the users and designers of the systems, not by the computers themselves. Users simply demand quicker results from more complicated computations.

Timing can be designed into computer systems, and sometimes must be, as when a computer is to be used to control real-time systems in the world. But the timing is engineered in by a designer or programmer who knows that the cycle time in this computer is N units, and that this action has to follow that action by M units, and, therefore, that a waiting period of M units or M/N cycles must be inserted between the command for the first action and the command for the second.

Timing considerations can enter into standard computational architectures only at the engineering level. They are not intrinsic to the architectures. Nor are they inherent in the mathematics or the theory behind those architectures. Consider the well-worn example of Turing machine theory, in which time is reduced to a sequence of discrete moments. Nothing in Turing machine theory depends on the computational steps having any particular timing, nor even any consistent timing. The theory would be unaffected if the first step took 2 milliseconds, the second took 5 years, the third one hour, and so on. Formal computations on formal symbols call for sequence. Action and interaction require timing (Bickhard & Terveen, 1995).

Building a clock into the system, as we do with computers, might seem at first blush a way to get timing into the architecture. But there are two problems with this approach. Human engineers and programmers know what clock signals mean, but for the system to be able to use them for timing purposes, it would have to know what they signal. A general system would have to distinguish timing signals from those for sound or pain or muscle stretching; treating timing signals as timing signals involves the very representational issues that we began with. Treating timing signals as timing signals requires that the system be capable of representation, and here we are back to square one. We have already argued that representation is impossible unless the system already has timing capabilities. Once again, we run up against the circularity of requiring representation in order to get representation.

The second problem with the clock "solution" to the timing problem is that such an architecture is extraordinarily brittle. Almost any change will destroy its overall functional integrity. New additions to such an architecture must bring with them new connections to the clock. From an evolutionary perspective, requiring simultaneous architectural additions is fatal. The simultaneity is of vanishingly low probability, especially when we consider a sequence of evolutionary changes. So the single-clock architecture is impossible for an evolved or evolving system.

Oscillations and modulations. There is an alternative, however: build timing right into the functional form of processing in the system. Instead of having one central clock, put clocks everywhere, and realize functional relationships as interactions among them. Clocks are, in essence, oscillators, so this proposal becomes: use an architecture of oscillatory processes that modulate one another. In the oscillatory architecture, input timing signals do not need to be interpreted. Timing is intrinsic to the process, and changes in the system architecture intrinsically involve changes in the timing provisions. If this view is correct, it is no accident of evolutionary implementation that the central nervous system functions in this way. An architecture supporting modulations among oscillations as the basic functional relationship is forced by the interactive nature of representation (Bickhard, 1991a; Bickhard & Terveen, 1995).

To forestall misconceptions about the formal power of an oscillatory architecture, let us note that an extreme version of modulation is for one system to modulate another ON or OFF. That is, a switch is a limiting case of modulation. Consequently, since a Turing machine can be constructed from switching relationships, this modulatory architecture is at least as powerful as Turing machines. Intrinsically handling timing makes it more powerful than Turing machines (Bickhard & Terveen, 1995).

The Central Nervous System. The interactive model requires an architecture of modulations among oscillatory processes. In striking convergence, that is precisely what we find in the central nervous system. In fact, evolution has created an impressive variety of modulatory relationships. Before turning to the next architectural requirement -- that of microgenesis -- we would like to demonstrate this convergence of functional architectural principles.

To begin with, non-zero baseline levels of endogenous oscillation are characteristic of many neural process, within single cells and over entire networks. There is ongoing oscillatory activity, not just responses to signals impinging on neurons (Gallistel, 1980; Kalat, 1984; Kandel & Schwartz, 1985; Thatcher & John, 1977). Such intrinsic activity can have no meaning and no explanation within symbol manipulation or connectionist approaches, because under either conception, system responses are triggered by inputs (Bickhard & Terveen, 1995).

Modulations among such oscillatory processes are ubiquitous. Indeed, there are multifarious types of such modulatory relationships. Cell and network oscillations modulate other cells and networks (Dowling, 1992; Thatcher & John, 1977).[15] Some messenger chemicals modulate the effects of others (Bloom & Lazerson, 1988; Cooper, Bloom, & Roth, 1986; Dowling, 1992; Fuxe & Agnati, 1987; Hall, 1992; Siegelbaum & Tsien, 1985).

Many neurons fire rarely or not at all (Bullock, 1981; Roberts & Bush, 1981). Instead, they propagate slow-wave ionic potentials, which affect ionic concentrations in extra-cellular spaces, or they modulate the graded release of neurotransmitters (Bullock, 1981; Fuxe & Agnati, 1991b). Both effects serve to modulate the modulatory effects occurring at classical synaptic junctions -- they modulate modulations.

There is, in fact, a broad array of non-synaptic modulatory influences (Adey, 1966; Fuster, 1989; Fuxe & Agnati, 1991a; Vizi, 1984). These range from slower, large-volume influences to fast, very local influences. Volume transmitters, for example, affect the activity of local volumes of neurons, not just single neurons on the receiving side of a synapse (Agnati, Fuxe, Pich, Zoli, Zini, Benfenati, Härfstrand, & Goldstein, 1987; Fuxe & Agnati, 1991a; Hansson, 1991; Herkenham, 1991; Matteoli, Reetz, & De Camilli, 1991; Vizi, 1984). Such slow, large volume modulations can meta-modulate the oscillatory and modulatory activity already occurring within neural networks, even to the point of effectively reconfiguring the effective neural circuitry (Dowling, 1992; Hall, 1992; Iverson & Goodman, 1986; Koch & Poggio, 1987). At the extreme of fast, local influences we find gap junctions, which transmit electrical changes from cell to cell virtually instantaneously, without mediating transmitters (Dowling, 1992; Hall, 1992; Nauta & Feirtag, 1986).

An insight that affords understanding of these influences is that messenger chemicals, including classical synaptic transmitters, are strongly related to hormones (Acher, 1985; Emson, 1985; Scharrer, 1987; Vizi, 1984, 1991). Hormones can be viewed as general information transmitting molecules -- as molecules that modulate multiple activities. Hormones exhibit an evolution from intracellular messengers to neurohumors to neurohormones to endocrine hormones (Hille, 1987; Turner & Bagnara, 1976). Many molecules, in fact, function at all of these levels in different parts of the body. Classic neurotransmitters, in this view, are just hormones that are local to the synaptic cleft.

Some systems propagate influences primarily via axonal impulses -- the visual tract, for example (Koch & Poggio, 1987) -- while others rely more on slow-wave potential movements. Local and volume transmitters seem to coexist throughout much of the brain (Fuxe & Agnati, 1991a; Vizi, 1984), and some synapses have been found to release multiple messengers that provide multiple levels of modulatory influence.

A striking aspect of these findings is the variety of types, and volume and time scales, of modulatory influences available in the central nervous system. There is a full evolutionary tool box of such influences, and the architectural requirements of symbol manipulations bear no relation to any of them. Neuroscientists are recognizing, in fact, that a conceptual shift will be required if such aspects of brain functioning are to be understood (Bullock, 1981; Freeman & Skarda, 1990; Pellionisz, 1991). Yet, such a modulatory tool box is precisely what would be expected from the interactivist perspective, with its necessity for ubiquitous timing influences. It is striking that the in-principle architectural considerations of interactivism and recent empirical central nervous system research converge on these oscillatory and modulatory principles.

Microgenesis. Not only do we need built-in timing in our architecture, we need microgenesis. Microgenesis is not a familiar term, so we present what we mean by it from several different perspectives. Roughly, we mean a certain kind of micro-level constructive process in the system. Microgenesis is constructive in that it creates conditions in the system that were not present prior to the construction; it is "micro" in that these constructions are "for the sake of" immediate ongoing activity of the system, not for constructive learning or development (which, by contrast, could be called "macrogenetic"). Our sense of microgenesis seems akin to what Werner and Kaplan (1963; Hanlon, 1991) originally meant by the term.[16] We also find a convergence with recent work by the Genevan functionalists (see below).

In developmental psychology, microgenesis is currently understood by many investigators to mean development or learning in the short run, and "microgenetic studies" are taken to mean short-term longitudinal studies involving repeated solution of the same types of problems (Inhelder et al., 1976; Karmiloff-Smith, 1986; Schmid-Schönbein, 1985; Siegler & Jenkins, 1989). We are concerned here with the ontology and architecture of the system and its processes, not with methodological approaches (however desirable they might be) to studying that system. As will become apparent below, microgenesis in our sense happens whenever the system functions, and development and learning processes modify microgenetic processes (cf. Hanlon, 1991). So we do not consider microgenesis to be a short-term version of learning or development.

The basic point is that a particular physical level system, or part of a system, must function in differing modes at differing times. This should not be a mysterious conception -- the CPU in a standard digital computer functions in different modes. In a real time interactive system, such shifts in manner of functioning must go on continuously. There must be processes that shift the manner of processing and set up new modes. In other words, there must be microgenetic processes.

Sometimes shifts in mode are called "activation." But microgenesis does not merely "energize" a fixed or isomorphic structure. Activation requires that what is activated be already complete, though functionally quiescent -- activation simply "turns it on." The activation view is compatible with a model of system functioning in which the available manners of functioning are embodied in a library of programs, and shifts in functioning are accomplished by "loading" or "activating" ready-made programs from the library. Microgenesis is not retrieval from a library of fixed programs; it is more like a constructive process that generates programs (or components and features thereof) "on the fly."

The notion of microgenesis has some kinship to the sense in which a single physical computer will function differently depending on which program it is running, but it has more kinship with the sense in which the central processing units of a computer must be continuously set up and re-set up to correctly handle the various different machine language instructions as those instructions flow into the processors. A given processor might add or shift or store bit patterns, and it must be "microgenetically set up" to do whatever it is that is needed at that point in the overall program.

In the brain, something similar occurs. The manner of processing in the brain -- or in a specific part of it -- will vary widely from time to time, from moment to moment, depending on what is being thought about, on what is being attended to, on what is demanding attention, on what interactions are being engaged in, and so on. These shifts in functional modes or manners of processing take place within a single physical-level system, so they require some sort of ongoing microgenetic set-up process to bring them about. The point is not simply that the brain can do different things. The brain can function in differing ways, and microgenesis is the process of shifting to, or setting up, alternative ways of functioning.

Recall from memory -- for example, while one is engaged in a complex but well learned task -- is not simply the readout of stored actions. Recall involves some process of creating differing patterns of functioning at differing times under the control of whatever the biochemical ground for memory storage might be. At differing points in a complex task, the brain is prepared for differing environmental conditions and ensuing courses of interaction. The actual course of interaction will depend, among things, on contingent details of the environment, AND on the specifics of that internal preparation for some class of possible courses of interaction. For example, if the conditions appropriate to a much later step in a complex task were to suddenly appear early in the task, the preparations would not be in place. There would, at the very least, be a startle response, and most likely the person would conclude that something seriously wrong had occurred. Microgenesis is the process of creating those internal preparations for various possible environmental conditions and ensuing courses of interaction. Such preparatory conditions will vary continuously throughout the course of a (complex) task, so the microgenesis of those preparatory conditions will also be continuous.

In automata-theoretic terms, it is not so much that a system makes a transition from one pre-existing state to the next pre-existing state. Rather, the states of the machine are possible states of the entire machine. These states differ in how they will interact with various possible inputs. "Movement" from one state to another is in fact a microgenetic construction of the machine conditions that constitute the next machine state, followed immediately by microgenetic preparations for the machine states that might come after it, and so on.

Microgenesis in our sense, then, is the construction of system modes and manners of processing. Microgenesis is implicit in both machine theory and brain studies. Usually, though, it is not accorded direct functional importance or accepted into the architecture; it is relegated to implementational levels and thenceforth ignored. We will argue, on the contrary, that microgenesis at the architectural level is critically important for learning.

There will be microgenesis in any system that changes its manner of functioning internally. But it will remain trivial in any system whose changes are trivial. And it will be theoretically unimportant in any system so long as the modes of functioning that are set up by the microgenetic processes are of interest but the "set up" processes are not. Interactivism forces us to focus on microgenesis because the modes of oscillation and modulation in the brain must change, and because, we will argue, learning and development must ultimately be constituted as changes in microgenetic processes.

We have argued that representation cannot be fundamentally a matter of correspondences or encoding relationships. Rather, it must take the form of organized indications of potential further interactions. We have argued that learning must involve error, that error signals must come from outside the learning system, and that learning must be ultimately based on blind variation and selection. We have explored the kind of computational architecture necessary for systems capable of interactive knowing and learning, and shown that suitable architectures must incorporate timing (in the form of modulatory relationships between oscillators) and microgenetic processes for shifting between computational modes and setting up new ones. All of these considerations are preliminaries to the central problem we are addressing in this paper.

We turn now to more general characterizations of learning and development, not just the blind variation and selection that take place at the limit. We turn to learning and development that do involve prior knowledge, at least heuristic knowledge, of what worked in the past.

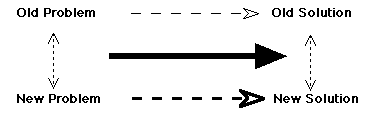
In a nutshell, heuristic problem solving requires nearness information for old and new problems, and for solutions or attempted solutions to those problems -- and that is topological information.[17] It turns out that oscillatory processes and microgenetic processes provide the basis for such topologies.

The learning system must somehow determine the similarities on the left between the problems, then use the relationship between the old problem and old solution (on top) to carry out the process indicated by the bold arrow in the middle -- constructing a new (attempted) solution that has similarities to the old solution that correspond to the similarities between the new problem and the old problem. Every arrow in this diagram is of interest to cognitive psychology, but we wish to focus on the nature and possibility of the dashed vertical arrows -- the relationships of similarity.

Problem spaces. On first impulse, one might try to capture these similarity relations by encoding all of the relevant information about potential problems and potential solutions. That is exactly what information-processing modelers do when they take problem solving to be search within a problem space. Classical presentations of this approach can be found in the General Problem Solver, and in its various successors, like SOAR (Ernst & Newell, 1969; Newell & Simon, 1972; Laird, Newell, & Rosenbloom, 1987; Newell, 1990). In the problem-space approach, all possible initial conditions, solution conditions, and intermediate conditions are treated as a set of problem states; those states, in turn, are considered to be interconnected by the possible moves or changes permitted by the nature of the problem. Collectively, the states and the possible transformations from one to another form the problem space.

Problem solving, in this classical sense, consists of identifying the initial conditions in the space, and seeking a path from an initial state to a solution state in which every step is an allowable transformation of the problem conditions. The problem states can be thought of as points. The permissible transformations can be thought of as arrows connecting pairs of points, indicating that the conditions of the point at the tail of the arrow can be transformed into the conditions of the point at the head of the arrow by the transformation that labels the arrow. Solving a problem, then, consists of finding a path of arrows from start state to solution state. The conception of problem solving as search in a problem space is foundational to information-processing models of cognition (Newell, 1980b; Bickhard & Terveen, 1995).

In such models, encoded features of problems and features of solutions could organize the spaces of potential problems and potential solutions that would allow the relevant similarities to be computed. In consequence, maps between problem and solution spaces can be computed. The system might "learn," for example, that whenever a current state has feature X, then transformation Q should be applied. In so doing, it generalizes across problem states in terms of a dimension of the associated feature space. In order to construct one link in the chain of transformational arrows that constitutes the solution, the system groups states with feature X as "nearby" (in this example, it actually treats them as equivalent).

Expert systems can supply more complicated examples. Clancey (1985) has shown that many expert systems function by heuristically classifying problems into predefined problem categories, with associated correspondences to predefined solution categories. Not all of the steps in such a process are always explicit in the program, but they are involved in the logic of the program. In more complex programs, either the problem space or the solution space, or both, may be a combinatoric space, in which the particular problem classifications or solution categories, or both, are constructed out of a basic set of predefined components (Clancey, 1992). Clancey shows that these may be understood as constructions of models of the systems being analyzed, or in which the problem is to be solved.

Our concern is that, even in these most sophisticated problem-solving programs, the representational capacities are limited to combinations of predefined components, or -- worse yet -- to predefined categories with no combinatoric possibilities. This is just a higher level version of the restriction to combinations of predefined representational atoms that characterizes the encoding approach in general. We will focus on how a system can generate its own new representations and its own new representational spaces.

Analogical reasoning. Our diagram with its mappings should bring to mind the information-processing approach to analogical reasoning that has been popular for the past decade, starting with Gentner's (1983) structural theory of analogies. Related conceptions can be found in Holland, Holyoak, Nisbett, and Thagard (1986) and increasingly among developmental psychologists as well (Gentner, 1988; Goswami, 1991; Halford, 1992). An analogy, for Gentner (1983), is a mapping from a source structure of elements to a target structure of elements that "aligns" or places in correspondence the elements and their structural relationships. For instance, "human" can be mapped to "horse" and "baby" to "foal"; the relationship between "human" and "baby" will also be mapped to the relationship between "horse" and "foal." In the construction of analogies, alignments of relations are more important than alignments of elements, though relational alignments may be discovered via initial trial alignments of elements.

Gentner's model is articulated within a standard symbol manipulation framework. Analogy is modeled as the construction of an isomorphism (or homomorphism) between data structures composed of encoded elements and their encoded relations (Falkenhainer, Forbus, & Gentner, 1989; Gentner & Markman, 1995). No analogy can be drawn unless both sides of the comparison, the source and the target, are available as encoded symbols (and, of course, unless the structures are so organized as to allow the right correspondences to be drawn). Clearly, this constitutes a fundamental difference between her approach and our own.

Nevertheless, Gentner's notion of isomorphism between representational structures is intrinsically dependent on the relational organization of those structures: the isomorphisms preserve precisely that relational organization (Falkenhainer et al., 1989; Gentner, 1983; Gentner & Markman, 1995). This emphasis on the relational organization of representation is convergent with the interactivist conception of representation as webs of interactive indicative relationships. Gentner's view, however, that the elements in these representational structures are themselves representations is a pure encodingist conception, and so is the notion that the relations are inherently representational (for instance, they might stand for causal relations; Falkenhainer et al., 1989). The other end of such presumed representational correspondences -- what is represented -- is not functionally available to the workings of the system (Fodor, 1981b). Consequently, all processing, including whatever is required for analogy, must be dependent solely on the type of the elements and the structural relations among those elements. At this level of description, the theory is a purely syntactic conception of analogy; only formal features of the structures of elements matter.[18]

Holland et al. (1986), in an attempt to introduce additional pragmatic considerations, relax the mapping requirements somewhat, and attempt to take into account the problem-solver's goals. Like Gentner (1983), they pay special attention to the temporal and causal relations in the source and target structures. According to Holland et al.,

Analogical problem solving involves four basic steps. These are (1) constructing [encoded] mental representations of the source and the target; (2) selecting the source as a potentially relevant analog to the target; (3) mapping the components of the source and the target (that is, identifying components that play corresponding roles in the two situations); and (4) extending the mapping to generate rules that apply to the target in order to achieve a solution. (1986, p. 292)

For workers in the field of analogical reasoning, this barely needs reciting; it is close to a truism. In terms of the problem we are trying to solve, however, all of these accounts of analogical reasoning run into the same difficulties. If not all mental representations are encodings, step (1) falls by the wayside. And without step (1), the explicit mapping of components called for in step (3) cannot happen. We are not denying the possibility of analogical reasoning in the manner described. It is perfectly possible to develop derivative encodings, in which one functional condition stands in for an interactive representation (Bickhard & Richie, 1983). Indeed, when we learn to read, or to make use of symbolic logic, we are learning encoding relationships: written words stand in for spoken words, and formal notation stands in for written statements in ordinary language.[19] We can learn those relationships only because we have already represented what is on both ends of them. Our ability to make and use analogies, however, is not limited to what we have derivatively encoded first. (This issue is never raised by the proponents of information-processing theories, because they assume that whatever we know we must have encoded.) For instance, as Holland et al. point out, many analogies that people make involve such `close' similarities that we consider them to be trivial, as in the case of thinking about the approach that a friend used when asking the boss for a raise, and the boss's reaction to that approach, when deciding how to ask for a raise yourself (1986, p. 309).

As is widely recognized, step (2), recognizing relevant analogs, is the real stumbling block, both in performing analogical reasoning, and in modeling it: "it is much easier to learn to map an atom onto a solar system than to spontaneously link the two analogs in the first place" (Holland et al., 1986, p. 315). Indeed so. Recognizing potential analogs is an instance of the very problem we have been posing -- the problem of functional and representational similarities -- in all of its glory. Within an information-processing approach (such as that of Anderson, 1983, or Holland et al. themselves), one solution that has been offered is to posit encoded representations in the form of semantic memory nodes or "concepts" and to envision activation passing from concept to related concepts along reified associative links (Collins & Quillian, 1969). But where do such "concepts" and links come from? They are not generated by the system; they have to be supplied for it by the designer or the programmer.

Consider the currently popular idea of "pragmatic reasoning schemas" (Cheng & Holyoak, 1986). For instance, Halford (1992) claims that children learn to solve Piaget's class-inclusion problem by forming an analogy between class-subclass relationships and a family schema (dog and cat are to animal as children are to parents). Though we can accept this as a plausible analogy, we cannot accept the underlying account of how children represent either kind of relationship in the first place, and how they come to treat one relationship as similar to the other. If Halford's (1992) account is true, children have to know both ends of the analogy, and they have to know them as structured encodings; otherwise there is no way to draw the necessary correspondences. But once children already have the right encodings of parent-child and class-subclass relationships, the correspondence encodings just fall out. (This is a general problem with encodings, in that everything is explicitly represented in them; they have no interesting implicit properties, no "surplus meaning.") Indeed, Halford has to posit processing loads that escalate with the number of terms in the relationship, because, otherwise, the correspondences between the relationships would have to be recognized as soon as the relationships are encoded (which, for Halford, means as soon as they are learned) and the class-inclusion analogy would develop no later than qualitatively simpler analogies do.

The fact that standard theories of analogical reasoning require that both terms of the analogy be encoded may explain why analogies that are perfectly straightforward from the modeler's point of view have often turned out to be quite difficult to grasp for participants in empirical studies, and require extensive hints to get across (e.g., Gick & Holyoak, 1980, 1983). Perhaps this is because the participants don't start out with the encoded representations that the experimenters presume they have; and if they don't, of course, they may not notice the correspondences that fall out once the right structures are given.

Encoding all of the information thus presupposes that our question has already been answered. Real problem-solvers do not start out with all of their information neatly laid out and predesigned. On the contrary, the real question is how the `similarity organizations' within spaces of potential problems and potential solutions can be functionally and constructively realized. Programming in the foundations for such organization, as a set of already encoded features, solves the problem for the system; it will never explain how a real system could solve the problem for itself.

Stimulus generalization. Indeed, the same general principles apply even to classical stimulus generalization. In stimulus generalization, the new stimulus is `similar' to an old stimulus, and the new response will be `similarly' `similar' to the old response. Pavlov's dog reacts to the bell similarly, but not identically, to the way it reacts to food, and it reacts to a slightly different bell similarly, but not identically, to the way it reacts to the first bell. Here the principles of organization are inherent in the nature and functioning of the system -- a sensory system, for example -- and not explicitly encoded and separately inputted by a programmer. There is no external programmer (save evolution) doing all of the work here, but there is nevertheless a fixedness of the generalization topologies involved, determined innately by the functioning of the sensory systems. In the general case, such topologies for generalization must somehow be realized in learned and developed cognitive spaces -- spaces that have been constructed by the system -- not just spaces that are available because they have been preprogrammed, or preformed at birth.

A metric presents a great deal of information about nearness and farness, similarity and dissimilarity. Often that is unavailable information. A metric organization is not to be expected in general, especially in early constructions of such problem and solution spaces when their internal organizations may still be unsettled. What, for example, is the metric distance from walking to bicycle riding, or, for that matter, from tricycle riding to bicycle riding, especially for someone who is just learning to ride a bicycle? What is the metric distance from playing the alto saxophone to playing the bass clarinet, for a musician who has never played a clarinet before? Furthermore, some problem or solution spaces do not logically admit distance measures. The relationships among the chemical properties within the rows and columns of the periodic table of the elements, for example, could not be usefully captured by a simple metric. The relationships across the columns of the table are not the same kind as the relationships across the rows -- there is an apples-and-oranges problem. Apples-and-oranges problems are all too common, and some comparisons are even worse -- more like apples and television sets. Single metric measures of comparison cannot be the most general form; something more general is required.

The most general formal approach to issues of nearness and farness is that of topology (Kelley, 1955; Hocking & Young, 1961). Algebra is the study of the points of sets, and the sorts of organizations induced by various transformations on those points. Topology is the study of subsets of sets, and the organizations inherent in the subset, intersection, and other set-theoretic relationships among them. The notion of `two points being near' in topology is roughly that of `two points being in the same (open) sets'.

Another form of organization, called a uniform space, has more structure than a topology, but less than a metric space (James, 1987). Uniform spaces are of deep importance in physics (Geroch, 1985), and may well be of fundamental importance in dealing with the issues at hand -- similarity relationships among cognitive constructions -- but the basic puzzle that we are focusing on is most easily stated in terms of topologies, whether or not they are also uniform spaces:

* How could a topology in a space of potential cognitive constructions be functionally realized in the actual constructive activities of the system?

* How could new topologies be generated in newly constructed spaces of potential cognitive constructions?

Note that the functional construction of such topologies in new cognitive spaces is among the most important steps in the construction of problem solving heuristics within and for those spaces. Once the topologies are available, the problem-solving heuristics are given in the continuous maps between such spaces.[20]

What is problematic for us here is not defining a topology as such. Abstract mathematical topologies are trivially easy to define. An unbounded number of topologies can be defined on an arbitrary underlying set, but nearly all of them will be irrelevant to any cognitive or constructive issues. The real problem here is to show how such a topology could: 1) emerge constructively in newly constructed cognitive spaces; 2) be functionally efficacious for the system, that is, functionally realized in the heuristic constructive processes that bring about new learning and problem solving; and 3) contain useful information that makes learning and problem solving work better.

Very few approaches to cognitive psychology even permit a meaningful definition of this problem of constructive topologies. Non-constructive approaches, like those of expert systems with predefined categories, clearly do not. Encoding-based conceptions can crudely address the topological issue per se -- via comparisons of features, for instance -- but cannot address the constructive emergence of such topologies. Of course, information-processing models, and, therefore, all of the dominant approaches in cognitive science and artificial intelligence are encoding-based. Models of learning and development within those fields are perforce extremely impoverished (Bickhard & Terveen, 1995).

Feature-based topologies. Information-processing conceptions run into fundamental difficulties when they try to address the problem of constructive topologies. Whether they use problem spaces or correspondences between structured encodings, the relevant topological information in information-processing models, when there is any, is static and predesigned for the system. How can the system construct new topologies? To up the ante, how could it construct new representational spaces with new topologies? The topologies that do get provided by information-processing models are seriously constricted. For instance, they might take the form of integer metrics on simple counts of feature overlaps: the distance between two points (in this perhaps simplest of all possibilities) would be defined as the number of features shared by the two points.

Existing critiques point out two problems with such models. First of all, they are static; not only must the feature space be supplied in advance, but it cannot be modified. Certainly multidimensional scaling models avoid accounting for changes in the dimensions of the spaces they model. Preset, inflexible category systems are a major problem for symbolic artificial intelligence; there is no way to transcend the "blindness" (Winograd & Flores, 1986) that comes from being locked into any particular categorical scheme.

Second, strict Euclidean feature models are incapable of accounting for asymmetric similarity judgments, such as the tendency to consider North Korea more similar to China than China is to North Korea. Nor can they account for other context-dependencies in similarity judgments, such as the fact that judgments of political similarity between countries may be different from judgments of geographical similarity. To deal with such judgments, Tversky (1977; Tversky & Gati, 1978) proposed a feature-based contrast model of similarity. The entities to be compared are first characterized as sets of features, then the feature sets are compared. Similarity is a function of the number of shared features minus the number of unshared features.

As Shanon (1988) was able to show in turn, appealing to features to explain similarity is fundamentally unsatisfactory. The feature-based model has to assume that the features are given in advance of the judgment of similarity; if not predefined once and for all, the features must at least be established independently of the similarity judgment to be undertaken. Moreover, the model accounts for context effects, for instance, effects of the goals of the person making the judgment, by supposing that selections are made among the preexisting features, or that differential weights are assigned to them. Because the range of possible contexts for similarity judgments is unbounded, Shanon (1988) argues, so is the range of possible context effects; if context works by selecting among preexisting features, there would have to be an infinite set of features already on hand. On the contrary, features are identified as the consequence of judgments of similarity:

Consider aunts inspecting their newborn nephews or nieces. Each aunt sees in the baby facial features resembling one of her ancestors. The same face will be associated with different features depending on which other faces it is being compared with. This pattern of behavior indicates that there is no given set of features by which a face is defined. What these features are is itself determined on the basis of an overall appraisal of similarity, or even a prior stipulation that similarity does in fact obtain. Thus, rather than similarity being determined by the sharing (and non-sharing) of features which are already given, the features are determined by the prior appraisal (or even stipulation) of similarity. (pp. 311-312)

Moreover, as Shanon points out, the featural model of similarity presumes that features are entirely independent of one another, and can be concatenated or added to one another without regard for interactions between them. And this assumption is no more tenable than the preceding ones. "One may wonder, for instance, whether the attributes `coin collector' and `introvert' are as independent as `coin collector' and `member of the Labor party' are" (p. 314).

Certainly the "feature" of weighing five kilograms is not independent of the "feature" of weighing ten kilograms, or of the "feature" of being prime or that of being a virtue or that of being a ternary relation, and so on and so on (Bickhard, 1987; Kenny, 1973). Filling out which properties and relationships are independent and which are not means filling out an entire metaphysics, something that is definitely not pre-encoded for many, perhaps most, genuine epistemic agents.

Shanon's (1988) argument amplifies our own critique of featural topologies, and hence of encoding-based conceptions of representation more generally. Neither metric spaces, nor the standard alternative to them, feature-based topologies, are adequate to account for judgments of similarity in particular, or for the role of similarity in developmental constructions more generally (for a review of some additional problems, see Medin et al., 1993). Features, when they can be identified, are identified on the basis of similarities which require further explanation. Information-processing approaches have not answered the question of how a system could learn topologies; they have tried to beg it.

Piaget and constructive topologies. Jean Piaget, on the other hand, never adopted prefabricated problem spaces, either metric or feature-based. And he took developmental processes -- constructive developmental processes -- far more seriously than any IP theorist has ever done. Yet he not only failed to solve the problem of constructive topologies -- key assumptions in his framework prevented him from posing the problem. Neither his assumption that knowledge consists of cognitive structures nor his view that development involves the equilibration of those structures permitted him to explore the issue of topologies.

Though Piaget would have rejected the physical symbol system hypothesis, his conception of knowledge did not succeed in breaking away from encodingism (Bickhard, 1988; Bickhard & Campbell, 1989). Piaget recognized two categories of knowledge. The less important kind, figurative knowledge (the sort that results from perception, or is found in mental images) is static, and represents by correspondence, and so cannot withstand our critique of encoding conceptions. Operative knowledge pertains to possible actions and consequently has an interactive flavor. However, Piaget maintained that operative knowledge, in the form of action schemes or logical structures, is isomorphic or "partially isomorphic" to structures in the environment, and consequently it, too, is encoded knowledge.

Though vestigial, and concealed within a subtle and sophisticated conception of representation, Piaget's encodingism undermines any attempt to construct a topology within his framework. And while his structures were intended to be dynamic systems, the mathematical structures (groupings, groups, and lattices) that he employed to model them are essentially static. A valid model of topologies in representational spaces cannot be founded on an untenable model of representation.

A more immediate obstacle to raising and resolving the problem of topologies, however, was Piaget's conception of developmental construction as the equilibration of cognitive structures. Equilibration is not a constructive process at all. It is a tendency toward equilibrium; that is, toward certain properties of the operative structures that get constructed (Bickhard, 1988; Campbell & Bickhard, 1992b). Piagetian constructions are of potential actions and potential meta-actions -- coordinations of actions. He was particularly concerned with the fascinating mathematical and logical properties that emerge when a space of potential meta-actions is constructively exhausted, producing a closed algebraic organization like a group. Piaget's (1985) model of equilibration never specified the processes of such construction, only some of the functional properties of the resulting constructions, like their reversibility or their tendency toward algebraic closure. Without such a model of the processes of construction -- of macrogenesis and microgenesis -- Piaget could not deliver a constructive topology.

Piaget would not have been able to produce a model of constructive processes in any case, because he rejected blind variation and selection, or trial and error, as the basis for cognitive evolution, or for learning and development. Hence he had no way to account for the emergence of heuristically guided variation and selection (Bickhard, 1988). Piaget was not all that interested in the details of problem solving. He preferred to ponder broad epistemological questions like the emergence of mathematical and logical necessity, for which he sought an explanation that would avoid the errors and inadequacies of both empiricism and nativism. Inspired by an analogy between physiological structures and their functions, on the one hand, and cognitive structures and their functions, on the other, he sought to understand the `embryological' (though not preformed) unfoldings of cognitive structures, and the consequent inherent emergence of algebraic closure in those structures. Structures that were algebraically closed consequently had other mathematically necessary properties, like those of group theory; Piaget proposed the emergence of such mathematically necessary properties as the solution to the epistemological mysteries of mathematical and logical necessity (Bickhard, 1988; Chapman, 1988; Kitchener, 1986; Piaget, 1971, 1985, 1987; Smith, 1993).

Piaget, then, was preoccupied with fundamental epistemological problems, and proposed that they could be solved by recognizing the properties toward which cognitive structures inherently tend. Such tendencies of construction, he believed, could be specified without providing any explicit model of the processes of construction. Without such an explicit model of construction, there could be no model of topologies in constructive spaces. Indeed, until the late introduction of functionalist ideas into his genetic epistemology (Inhelder & Piaget, 1979; Inhelder et al., 1976), Piaget was simply not very interested in learning or problem-solving activities, in heuristic problem solving or the use of information about previous successes when undertaking to solve new problems; throughout his career, he disparaged mere learning or "empirical abstraction" as having no significant constructive power. So the very issues that pose the problem of constructive topologies largely escaped his notice.

We have argued elsewhere that Piaget, despite valiant efforts, did not attain his primary goal of accounting for the emergence of the knowledge of logical necessity. At best, he could explain the origin of (algebraic) structures that possess various properties necessarily, but not knowledge of those properties or knowledge of their necessity (Bickhard, 1988; Campbell & Bickhard, 1986). An orthodox Piagetian is faced with a dilemma (see the case study presented by Smith, 1993, pp. 161-165). The Piagetian can deny that there is any distinction between structures that have necessary properties and knowledge that they are necessary. Or the Piagetian can acknowledge the distinction, and try to account for it by sharply differentiating developmental constraints that are obstinately assimilated to one another in Piaget's writings, such as constraints that are due to equilibration and those that are due to reflective abstraction.

Contrary to Piaget, we have argued that any framework capable of solving the epistemological problem of necessity must also be able to solve the problem of constructive topologies. A constructivist account of learning, based ultimately on blind variation and selection, is necessary to explain representation, and, ultimately, the development of necessity. But such a constructivist account must also be able to explain the variations and selections that are no longer blind, and that is the problem of constructive topologies.

Genevan functionalism. Piaget, then, was not primarily concerned with the questions that give rise to the need for constructive topologies, and could not have solved them even if they had captured his interest. By contrast, those latter-day Piagetians who have focused on the actual processes of problem solving, the Genevan functionalists, have been quite explicitly concerned with these questions. Retaining Piaget's conception of a scheme as the basic form of operative knowledge, they have cast the problem in terms of the generality of schemes, similarity between schemes, and similarity between the processes that construct schemes:

[t]he process of scheme formation tends toward generalization. If a scheme is triggered in a particular situation, it gets specified as a function of the context in such a way as to become relevant, but its epistemic enrichment and its heuristic value inhere in its ability to generalize to other situations. (Inhelder & de Caprona, 1992, p. 44)

Here we find a clear statement of the problem: old, already solved problems never recur in exactly the same form. So old solutions from old situations must somehow be generalized to fit new particular situations. Furthermore:

let us guard against thinking that familiar schemes could subsist, in the manner of pregiven ideas, as already constituted epistemic and heuristic units, at the disposal of a knowing subject who would only have to call them up and apply them directly. Vis-à-vis a novel situation, a scheme is a possibility for action, indeterminate, yet at the same time rich with virtualities of actualization...

In other words, a scheme has to be formed at a specific place and time by a process of microgenesis. The familiar character of a scheme is not given, it is to be constructed, and this elaboration means above all an appropriation of general schemes by the individual subject. Every familiar scheme is an individualized scheme. The particularities of the constructions which give rise to familiar schemes may not be the most important issue. The sort of psychology that paid close attention to them would have to devote itself to an endless description of particular constructions, themselves of an infinite diversity. The important thing is that the process of formation is a process of individualizing knowledge. (p. 44)

Generalizing from old situations to new situations cannot be accomplished by retrieval from some vast library of particularized schemes. Schemes must be adapted or generalized by a constructive process -- a microconstructive, or microgenetic, process.

In Inhelder and de Caprona's discussion we find a clear recognition of the need for generalization, and of the need for solving the problem of generalization within the framework of microgenesis. These issues have scarcely been recognized anywhere else.[21] Unfortunately, Inhelder and de Caprona do not supply any further constraints on, or characterizations of, a solution. An obstacle, we suspect, is the continued commitment to characterizing representation in terms of Piagetian schemes. At times in Genevan functionalist writings, schemes are considered psychologically real forms of mental representation; at other times, schemes are reduced to convenient descriptions of problems that children can solve or tasks they can accomplish. To the extent that schemes are still taken seriously as a basic kind of knowledge, they are vulnerable to critiques of encodings. To the extent that they are not, they need to replaced by some other conception of representation that the Genevan functionalists have not yet supplied.

We would now like to sketch a programmatic solution for the problem of constructive topologies. We base this solution on the interactive conception of representation and more generally on an approach that seeks to characterize psychological phenomena in process terms (Bickhard, 1980, 1992a, 1992d, in preparation-b; Bickhard & Richie, 1983; Campbell & Bickhard, 1986).

Overlap between constructive processes. The first step is to realize that constructive processes of any sort, macrogenetic or microgenetic, can induce functional topologies in the spaces of their possible constructions. In particular, the kind and degree of overlap between the constructive processes involved in the elements of such a space induce a topology on that space. The open sets of this topology are the sets of possible constructed elements that share various kinds and degrees of constructive process (incorporating information about kinds of process overlap might involve mathematical uniformities, not just topologies).

A conception strictly in terms of process overlap abstracts away from whatever principles of organization might be inherent in the microgenetic processes. Because topologies are induced by overlaps between constructive processes, those topologies will reflect the organizations of those microgenetic processes. Microgenetic processes might overlap in terms of their subroutines involved. They could overlap in various aspects, such as intensity or mood. They could overlap in illocutionary category or functional or grammatical category. Or they could overlap in amount of construction of some sort, such as degree of membership in fuzzy or prototypical categories. To chart all of the possible kinds of topologies would require a catalog of microgenetic processes and of the specifics of interactive representation in different domains.[22]

To develop an example a little farther, let us consider the microgenesis of words, which would include recalling them, saying them, using them in sentences, or writing them. In these contexts, some pairs of words share more microgenetic processes, or more differing kinds of microgenetic construction, than do other pairs of words. Suppose that the microgenetic preparation that has just been completed for a word already constructed does not have to be duplicated for another word that is under construction -- that is, that the products of microgenetic set-ups have some persistence, and do not need repeating so long as what has been set up is still available. Finally, suppose the free construction of words would honor this topology by obeying a "minimal effort" constraint: A tendency to minimize additional construction would favor the free construction of words that were `near' (share construction with) words that had been (recently) constructed. If our purpose were to present a detailed model of word microgenesis, a good deal more would have to be said in support of these suppositions. But all we need here is an illustration of microgenesis in general.

The point of our exercise is that such a model of word microgenesis would predict word associations. High overlaps in microgenetic processes lead to high probabilities of construction of `nearby' words given the prior construction of neighboring words. Associative "strength" is a manifestation of high degree of constructive overlap; the topologies of such associations are not explicit in the words, nor do they reside in any explicit links, arcs, or connections among those words. Instead, the topologies are intrinsic in the relationships of overlap in potential microgenetic constructions. Such an intrinsic topology is precisely the kind of functional relationship that is required for problem and solution spaces.

Manifested topologies. The associative net among words that results from overlaps in the microgenetic processes is a manifested constructive topology. Such manifested constructive topologies are not in the representations per se, nor are such topologies themselves represented. The topologies -- of associations in this example -- are implicit in the microconstructive overlaps; they have no other reality for the system. Hence there can be no flows of activation or energy along associative links in this model of associations. There can be no "spreading activation," and talk of "strengthening" or "weakening" links is at best metaphorical. It is the microgenetic constructive processes that are psychologically real; the `associations' are the manifest results of the implicit relationships among those constructive processes.

In such a model, the hyphens between Ss and Rs in an associative network, the links between the nodes, describe manifestations of implicit relationships in the microconstructive functioning of the system. They do not represent anything real in mental structure or process. Treating word associations as psychologically real is just another example of long-established predilections in psychology. Psychologists frequently reify relationships and properties into things, and take descriptions of possible task accomplishments as explanations of mental process (Campbell & Bickhard, 1986). Functional topologies will in general be implicit like this; they will not ontologically explicit like the nonconstructive encoded similarities that must be programmed into IP models.

Are stored computer programs sufficient? Recognizing that overlaps of constructive processes induce topologies in what is being constructed is a first step toward solving the problem, but it is not sufficient. Usually macrogenetic processes of development or learning are modeled as producing fixed structures -- e.g., computer programs -- which then engage in interaction with the world, and are filed away in some "memory" when not in use. Under such circumstances, there will be an induced implicit topology in the space of possible programs to be constructed, but there will be no particular functionally effective relationship between the old programs -- those already constructed and stored away for use -- and the new programs that still need to be constructed. The developmental constructive processes and the products that they construct are not of the same sort. Storing successful products of developmental construction can make those particular products available in the future, but storing developmental products cannot have any intrinsic effect on the developmental processes themselves.

Processes of development and learning, if they are to produce future constructions under heuristic guidance, need information about which construction processes have produced constructive products that worked. With no such information available in the developmental processes, and none in the stored products, the developmental constructive topology would be useless for heuristic problem solving because the already constructed successful problem definitions and solutions would have no particular location in, or relationship to, the constructive topology. There would be no anchors of success, of accepted problem-solution pairs, in the constructive space. Though accepted problem-solution pairs would be stored for future use, they would be past products, not current functional points in the constructive processes. New problems could not be related to old problems and their old successes because the old problems and successes would not be located in the developmental, or learning, topology. Problem and solution generalization could not occur because there would be no way to locate the points of success in the constructive space from which generalization could proceed.

To avoid this impasse, we need to recognize still another disanalogy between the brain and the computer: Programs are encoded and stored in a computer memory in all their detail, and then retrieved command by command as needed, but in the brain there is nothing akin to the particulateness of this process. Conversely, there is only marginal microgenesis for the stored programs in a computer (the shifting of the functional condition of the CPU). Once it has been acceptably written -- and, if necessary, compiled -- no further construction of a program is required to run it (although there will as a practical matter be much rewriting to fix bugs and improve functioning). Program development (programming) is functionally distinct from program microgenesis (CPU set ups), and, therefore, there is limited functional interaction between the two.

The activities of the brain, however, involve multiple modes of functioning of the various parts and regions of the brain, and these modes of functioning must be constructed on the fly. They must be constructed microgenetically, not retrieved like the next command in a computer program.

The disjuncture between macrogenesis (learning, development, programming) and microgenesis (setting up modes of functioning, setting up the CPU) is what must be transcended in order to make past successes in construction heuristically available for current problem solving. Without processes of microgenetic construction, there would be no way for the requisite generalization to take place during development and learning.

Shifts between modes of functioning. Microgenesis tracks and constructs needed modes of functioning throughout the course of action and interaction. Something must be `stored', of course, to direct the process. But the brain is massively parallel in its operations, and it functions by oscillatory interactions rather than particulate symbol manipulations. So whatever it is that gets stored in the brain to direct modes-of-functioning microgenesis is not going to much resemble a computer program.

From a slightly different perspective, the shifts of functional mode of a computer's Central Processing Unit are a form of microgenesis. Something roughly akin to this will have to be taking place continuously and massively in the brain, and everywhere in parallel. Microgenesis in the brain will be of modes of modulating oscillations. It cannot be an architecturally isolated particulate microprocess the way it is in the standard computer, in which processor, memory, and access between them are all architecturally distinct. All parts of the brain are capable of, and require, some form of variable microgenetic setup. Even processes that are already well learned are going to require microgenetic setup. Setups cannot be retrieved in discrete pieces like the instructions in a computer program. The microgenesis that goes on continuously throughout the nervous system is the locus of constructive topologies for development and learning.

Development and learning as modifications of microgenetic processes. What is the use for macrogenesis -- for learning and development -- of microgenetic constructions of modes of functioning that have already been learned? That is the key question linking topologies for learning and development to microgenesis. There is no question about the existence of a functional topology on the space of developmental constructions -- the constructive process itself already induces that. Obstacles arose when we tried to relate such a developmental constructive space to prior knowledge; to put it another way, obstacles arose when we tried to account for generalization from what has already developed or been learned. The obstacles can be circumvented if we realize that the to-be-learned and the already-learned are functionally linked via the microgenetic constructive processes for the already developed or learned knowledge.

From a microgenetic perspective, there is a simple difference between already-learned knowledge and as-yet problematic knowledge. The microgenetic process can already construct the previously learned knowledge; it cannot yet construct the knowledge that still needs to be learned. Development and learning, in other words, do not involve the storage of preconstructed structures or modes. Instead, they modify the microgenetic process so that it is able to prepare or set up those structures or modes when needed.[23]

So how can developmental constructions make use of information about past successes? Macrogenetic constructive processes must have their locus of operation in the microgenetic processes. The microgenetic processes do have available the information about past successes -- because they (re)construct those past successes when needed. So that information is resident in microgenetic constructive topologies: microgenetic processes are the common ground between the old and the new. Development and learning, then, must involve changes in those topology inducing microgenetic processes, in order to get access to old successes and change the way that new microgenetic constructions will proceed. Ultimately, the variations and selections that take place during the course of development must be variations and selections of microgenetic process.

Let us consider the operations of a digital computer from a microgenetic perspective. From this standpoint, all that the stored program really does is to direct the microgenesis in the CPU to go along setting up appropriate modes of functioning. Programming, the rough equivalent of development and learning in the computer framework, thus directs microgenesis in the CPU. In a standard computational architecture, of course, where every aspect is separated into distinct components and processes, only the programmer has access to the relevant constructive topologies.[24] Still, what gets changed during programming is the microgenetic processes in the CPU. Writing and rewriting programs (macrogenetic processes that are roughly analogous to development) modify the microgenetic constructive processes through variation and selection. Our basic logical points can be made, then, even in a relatively hostile architectural environment.

Within the interactivist microgenetic conception, the positions of already learned knowledge in the topology of potential constructions of new knowledge are intrinsically functionally available to learning and development. Variation and selection modify the microgenetic constructive processes, which naturally retain their constructive capacity for already learned knowledge.[25] Already learned knowledge will be constituted as (relatively) stable forms of functioning of the microgenetic processes. Insofar as the modifications made to microgenesis by learning and development are recursive (i.e., able to make use of previous changes within the microgenetic processes), those stable, already-learned forms of microgenesis will serve as the foundation, the framework, and the resources for further modifications to microgenesis by learning and development.

Because situations never recur in every level of detail, all interactions, even well learned ones, must be microgenetically constructed. Each instance of microgenesis will involve some degree of change in that microgenesis in sensitivity to the new characteristics of the new situation. We thus return to one of the major insights of Genevan functionalism (Inhelder & de Caprona, 1992). Every interaction, every microgenesis, involves learning (Clancey, 1993). Learning and development are not only located in microgenesis; they are ubiquitous in it.[26]

Interactivist problem and solution spaces. The construction of new problem characterizations, then, intrinsically involves a microgenetic topological relationship to already-learned problem characterizations. The solutions to those already-learned problem characterizations will likewise be intrinsically embedded in the space of possible microgenetic constructions of solutions to the new problem. The microgenetic link between the old problem (as characterized by the system) and the old solution already honors the constructive topology that can heuristically guide the microgenetic construction of a new potential solution to the new problem. The microgenetic constructive topology, then, implicitly provides the dashed vertical arrows in Figure 1, and the microgenetic constructive link from the old problem to the old solution provides the microgenetic link from the new problem to the new potential solution, so the processes of microgenesis give us the heavy dark horizontal arrow in the middle.

As in the word association example, the process of constructing the new problem representation will be related via the constructive topology to one or more old problems (otherwise it is a blind construction, without heuristic guidance). As the construction of solutions to the new problem is attempted, those attempted new solutions will tend to overlap microconstructively with the solution to the nearby old problem by virtue of the overlap between the old problem and the new problem. Because the relevant topologies are topologies inherent in the microgenetic constructive spaces themselves -- not distinct encoded topologies, like features, to be used by the constructive processes -- those topologies will be intrinsically functional in and for those microgenetic constructive processes.

The topologies are part of the dynamics of the system, rather than distinct encoded information to be used by the system. In comparable fashion, a connectionist net moves into (and perhaps within) an attractor in its dynamic space, and does not engage in search within an explicitly encoded space (Bickhard & Terveen, 1995; McClelland & Rumelhart, 1986; Rumelhart, 1989; Rumelhart & McClelland, 1986; Smolensky, 1986, 1988; van Gelder, 1992).

Two advantages, for interactivism as for connectionism, are that dynamic spaces can manifest properties could not be captured by any finite set of encodings (Bickhard, in preparation-a; Bickhard & Terveen, 1995; cf. Shanon, 1988, on the unboundedness of features); and that dynamic spaces intrinsically generalize to trajectories in those spaces that the system has never engaged in before, and, therefore, cannot have been explicitly taught. This latter point is obviously central to our argument for the microgenetic locus of learning and development.

Analogy and Similarity, Again. Now that we are armed with a new conception of problem and solution spaces, we are able to readdress some of the issues involved in constructing analogies and similarities. There are some very interesting comparisons between recent literature and aspects of the interactive microgenetic framework.

In particular, it is becoming clear that creating analogies (and other comparisons) is a process, not simply an automatic recognition (Medin et al., 1993). This process demonstrates strong context-dependence in its outcomes, and, therefore, strong context-sensitivity in the process itself. Indeed, the creation of analogies undergoes elaboration and reorganization with experience, whether we are concerned about development within the life-span of an individual or the evolution of ideas within the history of a culture (Gentner & Rattermann, 1991; Gentner & Jeziorski, 1993; Medin et al., 1993; Gentner & Markman, 1995). In the context of a single task, a target domain might be representationally reorganized so as to improve the comparisons that can be made with a source. Over time spans of individual or historical development, resources for creating analogies, and criteria for good analogies, are subject to change (Gentner & Grudin, 1985; Gentner & Jeziorski, 1993). The process by which analogies are created, then, must be a constructive one (Medin et al., 1993). Furthermore, unless there is prescience about what to construct, it must operate by variation and selection.

Recognition of these properties of comparison processes has been driven by the data in multiple studies by many researchers. Such properties can be addressed within encoding-based IP frameworks. Gentner's structure mapping engine, for example, has some properties of a variation and selection constructive process (Falkenhainer et al., 1989; Gentner & Markman, 1995). But such approaches 1) are limited in their resources to combinations of already provided representational elements, and, therefore, cannot account for genuinely novel representations or representational comparisons, and 2) have been introduced in a strictly ad hoc fashion to address unanticipated phenomena in the data.

In contrast, these properties of similarity comparisons are logically forced by the interactive framework. Over the span of a single task, a variation and selection constructive process is microgenesis. The need for microgenesis, in the interactive approach, has been extensively argued. Over ontogenetic time spans, it is the reorganization of microgenetic processes through variation and selection that constitutes learning and development. Historical time spans introduce changes in criteria by which analogies are evaluated (Bickhard, 1991c) -- and, therefore, in the kinds of analogies that will be microgenetically constructed. There is nothing ad hoc about these aspects of the model, and they are not limited to combinations of predefined representational encodings.

The context sensitivity of similarity judgments turns out to be also intrinsic and necessary. It has been found, for example, that similarity groupings can vary depending on the set of items to be grouped. For instance, judgments about how to group Austria and Sweden can differ depending on the remainder of the list: "Austria, Sweden, Poland, Hungary" leads to groupings of Austria and Sweden, while "Austria, Sweden, Norway, Hungary" promotes the grouping of Austria and Hungary (Tversky, 1977; Tversky & Gati, 1978; Medin et al., 1993). Tversky (1977) proposes that properties useful for grouping are more salient, and, therefore, have a greater influence on judgments of similarity; in this case, political versus geographical principles of grouping. A related phenomenon leads to the proposal that properties that are not useful for differentiating within a context (e.g., properties held in common across elements of a comparison set) have little saliency, and, therefore, will have little influence on similarity judgments. In a different comparison set, however, those same properties may invoke strong differentiations, thus have strong saliency, and, therefore, have a strong influence on similarity judgments. Italy and Switzerland, for example, have lower similarity in the context of other European countries than in the context of European and American countries (Tversky, 1977). Here, again, is a phenomenon that, although it can be addressed in an information processing framework -- rules for appropriate context sensitivities can be attempted in a computer model -- it must be addressed in an ad hoc manner. In contrast, such sensitivity is deeply intrinsic to the interactive model.

Interactivism and Context Sensitivity. One of the functional grounds for the interactive model is differentiation: differentiation of implicitly defined environmental categories, differentiation of possible next processes within the system; and so on. One consequence of the basic role of differentiation is that there are no primitive names in this model: Names require interpreters who know what the names mean and what they refer to.[27] Interpreters, in turn, are epistemological agents of the sort we wish to model and account for. If names presuppose interpreters, and interpreters are epistemic agents, we are caught in a vicious circle when attempting to model any sort of epistemic agent. Names cannot be primitives in any consistent model of knowledge and knowing. Names as primitives are paradigmatic encodings (Bickhard, 1980; Bickhard & Campbell, 1992; Campbell & Bickhard, 1992a).

Differentiation, on the other hand, is intrinsically context sensitive. What gets differentiated by any particular process of differentiation will depend on the context in which that differentiation occurs. What will be useful for differentiation will correspondingly depend on the context in which the differentiation is to be made. Among other consequences, what will usefully serve to represent something -- since representation is fundamentally a matter of differentiations -- will depend on the context in which the representation is to occur. But that implies that representational microgenesis will vary in a context-sensitive manner. Consequently, so will topology and similarity. Representational aspects that are useful for differentiation will be useful for representation, and, therefore, will be aspects of the topologies within which similarity is examined. "Saliency," in this view, is inherent in the nature of representation, and, therefore, inherent in the nature of similarity.

Saliency is not inherent in any encoding model: representational atoms are intrinsically context independent. As noted earlier, rules for saliency can be attempted within an encoding framework, but they will be subject to the general limitations of encodingism, and they will be unavoidably ad hoc. Quite the opposite within the interactive framework.

We have revisited similarity and analogy because, notwithstanding our disagreements with the framework within which these phenomena are customarily modeled, the data have driven some researchers toward proposing context-sensitive constructive processes that operate by variation and selection (Medin, Goldstone, & Gentner, 1993). In essence, they have moved toward proposing microgenesis, though that term is never found in the IP literature.[28] Interactivism, by contrast, intrinsically requires microgenesis. The interactive framework arrives at microgenesis without any reliance on data about analogy or similarity, thereby making the properties of microgenesis independently available for accounting for such data. Interactivism is much more hospitable to constructivist intuitions than the encoding-based IP framework will ever be.

More broadly, interactivism requires that all cognitive phenomena be context-specific (e.g., Bickhard, 1980; Bickhard & Richie, 1983; Campbell & Bickhard, 1986; Bickhard & Campbell, 1992; Campbell & Bickhard, 1992a). Microgenesis is ubiquitous, and so are its properties. Indeed, there is an important respect in which a microgenetic approach to modeling is significantly more powerful than any encoding-based computational approach.

Inadequacies of behaviorism -- and of information-processing. It is generally understood today that a computational approach to modeling behavior and learning is more powerful than a strict behaviorist approach. What has not been appreciated is that a microgenetic modeling approach is comparably more powerful than a strict computational approach.

Behaviorism is fundamentally inadequate to model behavior because there is only a finite number of possible external stimulus and response pairs, whereas the possible functional relations that could be manifested between input and output for even simple internal system organizations can easily be unbounded . Behavioral potentialities that would require infinite lists of inputs and outputs to characterize can be captured by a trivial internal interactive system organization. In a similar sense, IP or programming models are comparably inadequate in modeling power because the possible system modes of functioning that could be constructed in a microgenetic dynamic space can be unbounded relative to possible encodings of system organizations -- i.e., programs. Each point in the space of possible dynamics of microgenesis is a distinct mode of functioning, a distinct "program," for the system, and that space may well be infinite, thus not capturable by any finite list of programs.

Behaviorism fails as an account of learning because internal system organization can easily generalize to interactions involving stimulus and response patterns and sequences that have never been encountered, and, therefore, never learned. Information-processing or computer models comparably fail as an account of learning because the microgenetic dynamics of the system also easily generalize in unbounded ways to interactive forms or microgenetic set ups or "programs" that have never been encountered, and, therefore, never learned.

The streams of Ss and Rs in behaviorism, and the explicit programs and data in information-processing models, must be transcended (Greeno & Moore, 1993). Just as trivial interactive knowing and learning processes can manifest unbounded potential S-R capacities, so can trivial microgenetic processes manifest unbounded potential programs. We need a level of modeling in which the generation of interactions, on the one hand, and the generation of forms (programs) of interaction, on the other, are each themselves products of a higher order process, points in the topological dynamics of a higher-order system. In either case, the functional potentialities of the higher order dynamics cannot be captured by any finite listing of potentialities at the lower level.

Further developments. There are a number of important aspects of the topology problem and the interactive, microgenetic approach to its solution that we will not address here -- most notably, an account of how a variation and selection process could operate on a microgenetic process (in this regard, however, see the constraint mentioned below). We suggest, however, that our proposal does provide a viable approach to the problem of topologies of learning and development, and we would like to note that explicitly recognizing functioning in terms of oscillatory interactions avoids several additional problems that a conventional attempt to fill out our approach would encounter.

Conditions for learning are simply conditions in which microgenesis, which is going on all the time, encounters ill-defined conditions of further microconstruction. Microgenesis sets up oscillatory and modulatory modes of functioning in the brain, and variations in microgenesis will generate variations in the forms of oscillatory modulations that occur. The microconstruction process, however, cannot stop to await further directions when it encounters ill-defined conditions, it just continues. And in continuing, it intrinsically honors the relevant heuristic topologies. Furthermore, functioning in terms of oscillatory interactions guarantees that such ill-defined processes can continue -- communicating oscillatory processes will modulate each other in some manner or another. In our model, there are no situations in which further functioning becomes impossible. By contrast, in an undefined condition in a program or an automaton, in which the system receives an input for which no next step is defined in the current system condition, the system simply halts. A further benefit is that oscillations and their modulatory effects can be crossed and superimposed. In a modulatory architecture, subsystems cannot "hang up" while each waits for messages from the other, or while one waits for an information channel to clear so that some message can be sent across it.

Interactivism and topologies. We have dealt broadly with two sets of architectural constraints: those imposed by interactive representation and those imposed by the need for constructive topologies if there is to be heuristically guided learning and development. The two sets of constraints converge. Interactivism forces constructivism by variation and selection at the level of learning and development, which will manifest its own intrinsic topologies. Interactivism forces a functional architecture of modulations among oscillatory processes, which are intrinsically embedded in a functional topology of the space of possible oscillations and modulations. Constructive topologies and oscillatory topologies are not the same, but they are strongly related.

Possible oscillations can be parameterized, e.g., by vectors of Fourier coefficients, and that parameter space provides an intrinsic base for a topology. Microgenetic processes will have to honor such oscillatory topologies, at least in the sense that microgenesis will be constructing various functional modulatory relationships among oscillations in one part of the brain and the oscillatory influences from other parts of the brain. Such modulatory relationships are not fixed by the oscillatory spaces, but they must function in relation to them, and, thus, are constrained by them. Modulations, and, thus, the microgenesis of modulatory relationships, are constrained by the organization of the oscillatory spaces and the architecture of interconnections in the brain that permits modulations among those spaces.

Conversely, the oscillatory topologies provide a physical topology with emergent functional properties -- the modulations of one oscillatory process by another -- and it is this simultaneity of topology at both the physical and the functional level that makes possible the construction of new organizations with their own topologies. The construction of new oscillatory and modulatory relationships and topologies is the construction of new functional relationships and topologies.

Because interactive representation is emergent in certain forms of functional relationships, those physical or biological topologies of oscillations and modulations visit themselves not only on the emergent functional relationships, but on the emergent representational spaces too. It is this unity of emergent realization of the representational in the oscillatory and modulatory that ultimately makes possible the construction of new topologies that are functional for problem solving, learning, and development.

It is the requirement that old successful constructions be functionally available to guide new constructions that forces a focus on microgenesis, not just on developmental and learning constructions. Old successes are microgenetic constructions that the microgenetic process has already settled into, while not yet solved problems involve constructions that intrinsically honor the topology of the microgenetic processes.

Note that microgenesis cannot anticipate how to correctly set up for a new problem. This is just blind variation and selection at the microgenetic level. Suppose, however, that the microgenetic processes are locally destabilized by ensuing error of appropriate kinds (what can constitute "appropriateness" is an interesting problem). The same microgenetic constructions will tend not to recur under the same conditions if those previous constructions have yielded error. Conversely they will be stabilized when error does not ensue. Then the microgenetic topology will become "pinned" or "anchored" -- stabilized -- at the points of constructive success. These pins or anchors will modify the overall topological space so that microgenetic constructions in regions near such anchors will tend to yield trial solutions that are similarly similar to the solutions to the old problems. That is, the locus of learning and development is the microgenetic processes, which perforce become modified by variation and selection processes.

Interactivism, then, forces variation and selection constructivism, oscillatory and modulatory architectures, and a focus on microgenesis. Collectively, these provide a basis for the topologies that learning and development require.

Artificial intelligence, cognitive science, and information-processing approaches, on the other hand, have never really noticed the problem, and have nothing to offer in response except the inadequate topologies of predesigned feature spaces. There is a kind of microgenesis going on in computers, but it occurs at a purely engineering level -- it is not understood as having any theoretical importance.

Artificial intelligence, information-processing approaches, and cognitive science are also constrained by their dependence on notions of encoded data, and notions of process as computations on such data. The richness of potential dynamics needed to solve the problem of topologies for learning and development is impossible within a framework of computations on encoded data that reduces microgenesis to an insignificant detail of implementation. And of course, all of these frameworks run afoul of the logical incoherence of encodings as a fundamental form of representation well before issues of process dynamics and learning and development can even be brought up. Because of these and corollary foundational limitations, standard approaches to cognitive studies are at, and will remain at, a fundamental impasse (Bickhard & Terveen, 1995).

We have proposed a programmatic solution to the problem of learning and developmental topologies. It turns on the recognition that topologies for development and learning must ultimately be understood as manifest constructive topologies in microgenetic processes. Constructive processes as such, be they microgenetic or otherwise, induce relevant topologies. The common locus of the already-learned and the yet-to-be learned in a common microgenetic process provides the necessary functional relationships between microgenetic constructions of old knowledge and constructive attempts at new knowledge. Macrogenesis is constituted as the variation and selection of microgenetic processes.

Explanations of learning and representation lie on the frontier of attempts to understand the nature of mind. We have argued that the general problem of learning and development cannot be solved within contemporary architectures. A satisfactory architectural approach must take into account processes of microgenesis and the constructive topologies manifested by such processes of microgenetic construction. Similarly, representation cannot be understood within contemporary approaches, all of which make the incoherent presupposition of encodingism. The interactive model of representation that we offer as an alternative not only avoids the incoherence of encodingism, and the impossibility of learning, it also forces strong constraints on the type of architecture that could support interactive representational processes. Those architectural constraints, in turn, provide precisely the microgenetic constructive processes and manifested implicit topologies that are required for genuine learning and heuristic problem solving. The kind of architecture that is logically required for interactive representation is also the kind of architecture logically required for interactive learning.

There is a strong convergence, then, between the architectural requirements of representation and those of learning and development. Representation requires oscillatory processes ongoingly engaged in modulating each other. The topologies that are intrinsic to such processes and to their ongoing microgenetic construction are precisely what is required for learning and development that can make use of prior learning and development. It is doubly apt, then, that the central nervous system manifests a rich array of oscillatory and modulatory functional architectures.

Adey, W. R. (1966). Neurophysiological correlates of information transaction and storage in brain tissue. In E. Stellar & J. M. Sprague (Eds.), Progress in Physiological Psychology (Vol. 1, pp. 1-43). New York: Academic Press.

Agnati, L. F., Fuxe, K., Pich, E. M., Zoli, M., Zini, I., Benfenati, F., Härfstrand, A., & Goldstein, M. (1987). Aspects on the integrative capabilities of the Central Nervous System: Evidence for `volume transmission' and its possible relevance for receptor-receptor interactions. In K. Fuxe & L. F. Agnati (Eds.), Receptor-receptor interactions. (pp. 236-249). New York: Plenum.

Anderson, J. R. (1983). The architecture of cognition. Cambridge, MA: Harvard University Press.

Aristotle. (1941). De anima [On the soul]. In R. McKeon (Ed.), The basic works of Aristotle (pp. 535-603). New York: Random House. (Originally published c. 325 BC)

Bickhard, M. H. (1980). Cognition, convention, communication. New York: Praeger.

Bickhard, M. H. (1982). Automata theory, artificial intelligence, and genetic epistemology. Revue Internationale de Philosophie, 36, 549-566.

Bickhard, M. H. (1987). The social nature of the functional nature of language. In M. Hickmann (Ed.) Social and functional approaches to language and thought (pp. 39-65). New York: Academic.

Bickhard, M. H. (1988). Piaget on variation and selection models: Structuralism, logical necessity, and interactivism. Human Development, 31, 274-312.

Bickhard, M. H. (1991a). Cognitive representation in the brain. In Encyclopedia of Human Biology (Vol. 2, pp. 547-558). New York: Academic Press.

Bickhard, M. H. (1991b). Homuncular innatism is incoherent: A reply to Jackendoff. The Genetic Epistemologist, 19(3), p. 5.

Bickhard, M. H. (1991c). A pre-logical model of rationality. In L. P. Steffe (Ed.), Epistemological foundations of mathematical experience (pp. 68-77). New York: Springer-Verlag.

Bickhard, M. H. (1992a). How does the environment affect the person? In L. T. Winegar & J. Valsiner (Eds.), Children's development within social context: Metatheory and theory (pp. 63-92). Hillsdale, NJ: Erlbaum.

Bickhard, M. H. (1992b). Scaffolding and self-scaffolding: Central aspects of development. In L. T. Winegar & J. Valsiner (Eds.), Children's development within social context: Research and methodology (pp. 33-52). Hillsdale, NJ: Erlbaum.

Bickhard, M. H. (1992c). Commentary [on the age 4 transition]. Human Development, 35, 182-192.

Bickhard, M. H. (1992d, June). Levels of representationality. Paper presented at the Workshop on the Science of Cognition, Santa Fe, New Mexico.

Bickhard, M. H. (1993). Representational content in humans and machines. Journal of Experimental and Theoretical Artificial Intelligence, 5, 285-333.

Bickhard, M. H. (in preparation-a). Interaction and representation.

Bickhard, M. H. (in preparation-b). The whole person: Toward a naturalism of persons. Harvard University Press.

Bickhard, M. H., & Campbell, D. T. (in preparation). Variations in variation and selection.

Bickhard, M. H., & Campbell, R. L. (1989). Interactivism and genetic epistemology. Archives de Psychologie, 57, 99-121.

Bickhard, M. H., & Campbell, R. L. (1992). Some foundational questions concerning language studies: With a focus on categorial grammars and model theoretic possible worlds semantics. Journal of Pragmatics, 17, 401-433.

Bickhard, M. H., & Richie, D. M. (1983). On the nature of representation: A case study of James J. Gibson's theory of perception. New York: Praeger.

Bickhard, M. H., & Terveen, L. (1995). Foundational issues in Artificial Intelligence and Cognitive Science: Impasse and solution. Amsterdam: North-Holland.

Block, N. (1986). Advertisement for a semantics for psychology. In P. A. French, T. E. Uehling, & H. K. Wettstein (Eds.), Midwest Studies in Philosophy X: Studies in the philosophy of mind (pp. 615-678). Minneapolis: University of Minnesota Press.

Bloom, F. E., & Lazerson, A. (1988). Brain, mind, and behavior. San Francisco: Freeman.

Brachman, R. J. (1979). On the epistemological status of semantic networks. In N. V. Findler (Ed.), Associative networks: Representation and use of knowledge by computers (pp. 3-50). New York: Academic Press.

Brown, J. W. (1988). The life of the mind. Hillsdale, NJ: Erlbaum.

Bullock, T. H. (1981). Spikeless neurones: Where do we go from here? In A. Roberts & B. M. H. Bush (Eds.), Neurones without impulses. (pp. 269-284). Cambridge: Cambridge University Press.

Campbell, D. T. (1974). Evolutionary epistemology. In P. A. Schilpp (Ed.), The philosophy of Karl Popper (pp. 413-463). LaSalle, IL: Open Court.

Campbell, R. L., & Bickhard, M. H. (1986). Knowing levels and developmental stages. Basel: Karger.

Campbell, R. L., Bickhard, M. H. (1987). A deconstruction of Fodor's anticonstructivism Human Development, 30(1), 48-59.

Campbell, R. L., & Bickhard, M. H. (1991). If human cognition is adaptive, can human knowledge consist of encodings? Behavioral and Brain Sciences, 14, 488-489.

Campbell, R. L., & Bickhard, M. H. (1992a). Clearing the ground: Foundational questions once again. Journal of Pragmatics, 17, 557-602.

Campbell, R. L., & Bickhard, M. H. (1992b). Types of constraints on development: An interactivist approach. Developmental Review, 12, 311-338.

Catán, L. (1986). The dynamic display of process: Historical development and contemporary uses of the microgenetic method. Human Development, 29, 252-263.

Chapman, M. (1988). Constructive evolution: Origins and development of Piaget's thought. Cambridge: Cambridge University Press.

Cheng, P. W., & Holyoak, K. J. (1985). Pragmatic reasoning schemas. Cognitive Psychology, 17, 391-416.

Christensen, W. D. (in press). A complex systems theory of teleology. Biology and Philosophy.

Christensen, W. D. (in preparation). From descriptive to normative functionality.

Clancey, W. J. (1985). Heuristic classification. Artificial Intelligence, 27, 289-350.

Clancey, W. J. (1992). Model construction operators. Artificial Intelligence, 53, 1-115.

Clancey, W. J. (1993). Situated action: A neuropsychological interpretation response to Vera and Simon. Cognitive Science, 17, 87-116.

Collins, A. M., & Quillian, M. R. (1969). Retrieval time from semantic memory. Journal of Verbal Learning and Verbal Behavior, 8, 240-247.

Cooper, J. R., Bloom, F. E., & Roth, R. H. (1986). The biochemical basis of neuropharmacology. Oxford: Oxford University Press.

Deacon, T. W. (1989). Holism and associationism in neuropsychology: An anatomical synthesis. In E. Perecman (Ed.), Integrating theory and practice in clinical neuropsychology (pp. 1-47). Hillsdale: Erlbaum.

Dowling, J. E. (1992). Neurons and networks. Cambridge, MA: Harvard University Press.

Dretske, F. I. (1981). Knowledge and the flow of information. Cambridge, MA: MIT Press.

Dretske, F. I. (1988). Explaining behavior. Cambridge, MA: MIT Press.

Edelman, G. M. (1987). Neural Darwinism. New York: Basic Books.

Edelman, G. M. (1992). Bright air, brilliant fire. New York: Basic Books.

Eilenberg, S. (1974). Automata, languages, and machines, Vol. A . New York: Academic Press.

Emson, P. C. (1985). Neurotransmitter systems. In D. Bousfield (Ed.), Neurotransmitters in action. (pp. 6-10). Amsterdam: Elsevier.

Ernst, G. W., & Newell, A. (1969). GPS: A case study in generality and problem solving. New York: Academic Press.

Falkenhainer, B., Forbus, K. D., & Gentner, D. (1989). The Structure-Mapping Engine: Algorithm and examples. Artificial Intelligence, 41, 1-63.

Fodor, J. A. (1975). The language of thought. New York: Crowell.

Fodor, J. A. (1981a). The present status of the innateness controversy. In J. Fodor, RePresentations (pp. 257-316). Cambridge: MIT Press.

Fodor, J. A. (1981b). Methodological solipsism considered as a research strategy in cognitive psychology. In J. Haugeland (Ed.), Mind design (pp. 307-338). Cambridge: MIT Press.

Fodor, J. A. (1987). Psychosemantics. Cambridge, MA: MIT Press.

Fodor, J. A. (1990). A theory of content and other essays. Cambridge, MA: MIT Press.

Fodor, J. A., Bever, T., & Garrett, M. (1974). The psychology of language. New York: McGraw-Hill.

Fodor, J. A., & Pylyshyn, Z. (1981). How direct is visual perception?: Some reflections on Gibson's ecological approach. Cognition, 9, 139-196.

Freeman, W. J., & Skarda, C. A. (1990). Representations: Who needs them? In J. L. McGaugh, N. M. Weinberger, & G. Lynch (Eds.), Brain organization and memory (pp. 375-380). Oxford: Oxford University Press.

Fuster, J. M. (1989). The prefrontal cortex. New York: Raven Press.

Fuxe, K., & Agnati, L. F. (1987). Receptor-receptor interactions. New York: Plenum.

Fuxe, K., & Agnati, L. F. (Eds.) (1991a). Volume transmission in the brain: Novel mechanisms for neural transmission. New York: Raven.

Fuxe, K., Agnati, L. F. (1991b). Two principal modes of electrochemical communication in the brain: Volume versus wiring transmission. In K. Fuxe & L. F. Agnati (Eds.), Volume transmission in the brain: Novel mechanisms for neural transmission. (pp. 1-9). New York: Raven.

Gallistel, C. R. (1980). The organization of action: A new synthesis. Hillsdale, NJ: Erlbaum.

Gentner, D. (1983). Structure-mapping: A theoretical framework for analogy. Cognitive Science, 7, 155-170.

Gentner, D. (1988). Metaphor as structure mapping: The relational shift. Child Development, 59, 47-59.

Gentner, D. (1989). The mechanisms of analogical learning. In S. Vosniadou & A. Ortony (Eds.),Similarity and analogical reasoning (pp. 199-241). Cambridge: Cambridge University Press.

Gentner, D., & Grudin, J. (1985). The evolution of mental metaphors in psychology. American Psychologist, 40(2), 181-192.

Gentner, D., & Jeziorski, M. (1993). The shift from metaphor to analogy in Western science. In A. Ortony (Ed.), Metaphor and thought (2nd ed., pp. 447-480). New York: Cambridge University Press.

Gentner, D., & Markman, A. B. (1995). Similarity is like analogy: Structural alignment in comparison. In C. Cacciari (Ed.), Similarity in language, thought and perception. Milan: Brepols.

Gentner, D., & Rattermann, M. J. (1991). Language and the career of similarity. In S. A. Gelman & J. P. Byrnes (Eds.), Perspectives on language and thought: Interrelations in development. (pp. 225-277). London: Cambridge University Press.

Geroch, R. (1985). Mathematical physics. Chicago: University of Chicago Press.

Gibson, J. J. (1977). The theory of affordances. In R. Shaw & J. Bransford (Eds.), Perceiving, acting and knowing (pp. 67-82). Hillsdale, N.J.: Erlbaum.

Gick, M. L., & Holyoak, K. J. (1980). Analogical problem solving. Cognitive Psychology, 12, 306-355.

Gick, M. L., & Holyoak, K. J. (1983). Schema induction and analogical transfer. Cognitive Psychology, 15, 1-38.

Ginzberg, A. (1968). Algebraic theory of automata. New York: Academic Press.

Goldberg, A., & Robson, D. (1983). Smalltalk-80: The language and its implementation. Reading, MA: Addison-Wesley.

Goswami, U. (1991). Analogical reasoning: What develops? A review of research and theory. Child Development, 62, 1-22.

Greeno, J. G., & Moore, J. L. (1993). Situativity and symbols: Response to Vera and Simon. Cognitive Science, 17(1), 49-69.

Halford, G. S. (1992). Analogical reasoning and conceptual complexity in cognitive development. Human Development, 35, 193-217.

Hall, Z. W. (1992). Molecular neurobiology. Sunderland, MA: Sinauer.

Hanlon, R. E. (Ed.) (1991a). Cognitive microgenesis: A neuropsychological perspective. New York: Springer.

Hanlon, R. E. (1991b). Introduction. In R. E. Hanlon (Ed.) Cognitive microgenesis: A neuropsychological Perspective (pp. xi-xx). New York: Springer-Verlag.

Hanson, P. P. (Ed.) (1990). Information, language, and cognition. Vancouver: University of British Columbia Press.

Hansson, E. (1991). Transmitter receptors on astroglial cells. In K. Fuxe & L. F. Agnati (Eds.), Volume transmission in the brain: Novel mechanisms for neural transmission. (pp. 257-265). New York: Raven.

Harnad, S. (1989). The symbol grounding problem. Physica D, 42, 335-346.

Harris-Warrick, R. M., Marder, E., Selverston, A. I., & Moulins, M. (1992). Dynamic biological networks. Cambridge: Cambridge University Press.

Hayes, P. J., Ford, K. M., & Adams-Webber, J. R. (1992). Human reasoning about artificial intelligence. Journal of Experimental and Theoretical Artificial Intelligence, 4, 247-263.

Herkenham, M. (1991). Mismatches between neurotransmitter and receptor localizations: Implications for endocrine functions in brain. In K. Fuxe & L. F. Agnati (Eds.), Volume transmission in the brain: Novel mechanisms for neural transmission. (pp. 63-87). New York: Raven.

Hille, B. (1987). Evolutionary origins of voltage-gated channels and synaptic transmission. In G. M. Edelman, W. E. Gall, & W. M. Cowan (Eds.), Synaptic function. (pp. 163-176). New York: Wiley.

Hocking, J. G., & Young, G. S. (1961). Topology. Reading, MA: Addison-Wesley.

Hofstadter, D. R. (1995). Fluid concepts and creative analogies: Computer models of the fundamental mechanisms of thought. New York: Basic Books.

Holland, J. H., Holyoak, K. J., Nisbett, R. E., & Thagard, P. R. (1986). Induction: Processes of inference, learning and discovery. Cambridge, MA: MIT Press.

Hooker, C. A. (1995). Reason, regulation, and realism: Toward a regulatory systems theory of reason and evolutionary epistemology. Albany, NY: SUNY Press.

Hopcroft, J. E., & Ullman, J. D. (1979). Introduction to automata theory, languages, and computation. Reading, MA: Addison-Wesley.

Houser, N., & Kloesel, C. (1992). The essential Peirce. Vol. 1. Bloomington: University of Indiana Press.

Inhelder, B., & de Caprona, D. (1992). Vers le constructivisme psychologique: Structures? Procédures? Les deux indissociables [Towards constructivism from a psychological standpoint: Structures? Procedures? Both inseparable.] In B. Inhelder & G. Cellérier (Eds.), Le cheminement des découvertes de l'enfant: Recherches sur les microgenèses cognitives (pp. 19-50). Neuchâtel: Delachaux et Niestlé.

Inhelder, B., & Piaget, J. (1979). Procédures et structures. Archives de Psychologie, 47, 165-176.

Inhelder, B., Ackermann-Valladão, E., Blanchet, A., Karmiloff-Smith, A., Kilcher-Hagedorn, H., Montangero, J., & Robert, M. (1976). Des structures cognitives aux procédures de découverte [From cognitive structures to procedures for discovery]. Archives de Psychologie, 44, 57-72.

Iverson, L. L., & Goodman, E. (1986). Fast and slow chemical signalling in the nervous system. Oxford: Oxford University Press.

James, I. M. (1987). Topological and uniform spaces. New York: Springer-Verlag.

Kalat, J. W. (1984). Biological psychology (2nd ed.). Belmont, CA: Wadsworth.

Kandel, E. R., & Schwartz, J. H. (1985). Principles of neural science (2nd ed.). New York: Elsevier.

Karmiloff-Smith, A. (1986). From meta-processes to conscious access: Evidence from children's metalinguistic and repair data. Cognition, 23, 95-147.

Kelley, J. L. (1955). General topology. Princeton, NJ: Van Nostrand.

Kenny, A. (1973). Wittgenstein. Cambridge, MA: Harvard University Press.

Kitchener, R. F. (1986). Piaget's theory of knowledge. New Haven: Yale University Press.

Koch, C., & Poggio, T. (1987). Biophysics of computation. In G. M. Edelman, W. E. Gall, & W. M. Cowan (Eds.) Synaptic function. (pp. 637-697). New York: Wiley.

Kripke, S. (1972). Naming and necessity. In D. Davidson & G. Harman (Eds.) Semantics of natural language (pp. 253-355). Dordrecht: Reidel.

Laird, J. E., Newell, A., & Rosenbloom, P. S. (1987). SOAR: An architecture for general intelligence. Artificial Intelligence, 33, 1-64.

Locke, J. (1961). An essay concerning human understanding. London: Dent. (Originally published 1690).

Loewer, B., & Rey, G. (Eds.) (1991). Meaning in mind: Fodor and his critics. Oxford: Blackwell.

Matteoli, M., Reetz, A. T., & De Camilli, P. (1991). Small synaptic vesicles and large dense-core vesicles: Secretory organelles involved in two modes of neuronal signaling. In K. Fuxe & L. F. Agnati (Eds.), Volume transmission in the brain: Novel mechanisms for neural transmission. (pp. 181-193). New York: Raven.

McClelland, J. L., & Rumelhart, D. E. (1986). Parallel Distributed Processing. Vol. 2: Psychological and Biological Models. Cambridge, MA: MIT Press.

Medin, D. L., Goldstone, R. L., & Gentner, D. (1993). Respects for similarity. Psychological Review, 100, 254-278.

Millikan, R. G. (1984). Language and other biological categories. Cambridge, MA: MIT Press.

Millikan, R. G. (1993). White Queen psychology and other essays for Alice. Cambridge, MA: MIT Press.

Murphy, J. P. (1990). Pragmatism. Chicago: Westview.

Nauta, W. J. H., & Feirtag, M. (1986). Fundamental neuroanatomy. San Francisco: Freeman.

Newell, A. (1980a). Physical symbol systems. Cognitive Science, 4, 135-183.

Newell, A. (1980b). Reasoning, problem solving, and decision processes: The problem space as a fundamental category. In R. Nickerson (Ed.), Attention and Performance VIII (pp. 693-718). Hillsdale, NJ: Erlbaum.

Newell, A. (1990). Unified theories of cognition. Cambridge, MA: Harvard University Press.

Newell, A., & Simon, H. A. (1972). Human problem solving. Englewood Cliffs, NJ: Prentice-Hall.

O'Hara, S. (1994). Towards a blackboard architecture for the solution of interpretive proportional analogy problems. Paper presented at the Florida Artificial Intelligence Research Symposium, Pensacola Beach, FL, May 5-7.

O'Hara, S., & Indurkhya, B. (1995). "Adaptation and Redescription in the Context of Geometric Proportional Analogies", pp. 80-86. In Adaptation of Knowledge for Reuse: Papers from the 1995 Fall Symposium, Technical Report FS-95-04, American Association for Artificial Intelligence, Menlo Park, California.

Palmer, S. E. (1978). Fundamental aspects of cognitive representation. In E. Rosch & B. B. Lloyd (Eds.), Cognition and categorization. Hillsdale, NJ: Erlbaum.

Pascoe, G. A. (1986). Elements of object-oriented programming. Byte, 11(8), 139-144.

Pellionisz, A. J. (1991). Geometry of massively parallel neural interconnectedness in wired networks and wireless volume transmission. In K. Fuxe & L. F. Agnati (Eds.), Volume transmission in the brain: Novel mechanisms for neural transmission. (pp. 557-568). New York: Raven.

Piaget, J. (1954). The construction of reality in the child. New York: Basic. (Originally published 1937.)

Piaget, J. (1971). Biology and knowledge. Chicago: University of Chicago Press. (Originally published 1967.)

Piaget, J. (1985). The equilibration of cognitive structures: The central problem of intellectual development. (trans. T. Brown & K. J. Thampy). Chicago: University of Chicago Press. (Originally published 1975).

Piaget, J. (1987). Possibility and necessity. Minneapolis: University of Minnesota Press. (Originally published 1981-1983).

Piattelli-Palmarini, M. (Ed.) (1980). Language and learning. The debate between Jean Piaget and Noam Chomsky. Cambridge: Harvard University Press.

Putnam, H. (1975). The meaning of meaning. In K. Gunderson (Ed.), Language, mind, and knowledge. Minneapolis: University of Minnesota Press.

Putnam, H. (1990). Realism with a human face. Cambridge, MA: Harvard University Press.

Putnam, H. (1992). Renewing philosophy. Cambridge, MA: Harvard University Press.

Pylyshyn, Z. (1984). Computation and cognition. Cambridge, MA: MIT Press.

Radnitzky, G., & Bartley, W. W., III. (Eds.) (1987). Evolutionary epistemology, theory of rationality, and the sociology of knowledge. LaSalle, IL: Open Court.

Reeke, G. N., & Edelman, G. M. (1988). Real brains and artificial intelligence. Daedalus, 117(1), 143-173.

Roberts, A., & Bush, B. M. H. (Eds.) (1981). Neurones without impulses. Cambridge: Cambridge University Press.

Rosenthal, S. B. (1983). Meaning as habit: Some systematic implications of Peirce's pragmatism. In E. Freeman (Ed.), The Relevance of Charles Peirce (pp. 312-327). La Salle, IL: Open Court.

Rosenthal, S. B. (1987). Classical American pragmatism: Key themes and phenomenological dimensions. In R. S. Corrington, C. Hausman, & T. M. Seebohm (Eds.) Pragmatism considers phenomenology (pp. 37-57). Washington, DC.: University Press.

Rosenthal, S. B. (1990). Speculative pragmatism. LaSalle, IL: Open Court.

Rumelhart, D. E. (1989). The architecture of mind: A connectionist approach. In M. I. Posner (Ed.) Foundations of cognitive science (pp. 133-160). Cambridge, MA: MIT Press.

Rumelhart, D. E., & McClelland, J. L. (Eds.) (1986). Parallel Distributed Processing. Vol. 1: Foundations. Cambridge, MA: MIT Press.

Sahley, C. L. (1993). Review of Dynamic biological networks. Science, 260, 244.

Scharrer, B. (1987). Evolution of intercellular communication channels. In B. Scharrer, H.-W. Korf, & H.-G. Hartwig (Eds.), Functional morphology of neuroendocrine systems (pp. 1-8). Berlin: Springer-Verlag.

Schmid-Schönbein, C. (1985). "He, sind ja beide gleich groß!" Eine prozeßanalytische Rekonstruktion des Verständnisses von "gleich sein" ["Hey, they're both just as big!" A process-analytic reconstruction of the understanding of "the same"]. In T. B. Seiler & W. Wannenmacher (Eds.), Begriffs- und Wortbedeutungsentwicklung [Development of word meaning and comprehension.] (pp. 167-189). Berlin: Springer.

Schweiger, A. (1991). Reflections on perception and action. In R. E. Hanlon (Ed.) Cognitive microgenesis: A neuropsychological perspective (pp. 92-105) New York: Springer-Verlag.

Shanon, B. (1988). On the similarity of features. New Ideas in Psychology, 6, 307-321.

Siegelbaum, S. A., & Tsien, R. W. (1985). Modulation of gated ion channels as a mode of transmitter action. In D. Bousfield (Ed.), Neurotransmitters in action. (pp. 81-93). Amsterdam: Elsevier.

Siegler, R. S. & Jenkins, E. (1989). How children discover new strategies. Hillsdale, NJ: Erlbaum.

Slezak, P. (1992, June). Situated cognition: Minds in machines or friendly photocopiers? Presented at the workshop on The Science of Cognition, Santa Fe, New Mexico.

Slezak, P. (1994). Situated cognition: Empirical issue, `paradigm shift', or conceptual confusion? In A. Ram & K. Eiselt (Eds.), Proceedings of the Sixteenth Annual Conference of the Cognitive Science Society (pp. 806-811). Hillsdale, NJ: Erlbaum.

Smith, B. C. (1987). The correspondence continuum. Report No CSLI-87-71. Center for the Study of Language and Information, Stanford University, Stanford CA.

Smith, L. (1993). Necessary knowledge: Piagetian perspectives on constructivism. Hove, England: Erlbaum.

Smolensky, P. (1986). Information processing in dynamical systems: Foundations of Harmony Theory. In D. E. Rumelhart & J. L. McClelland (Eds.), Parallel Distributed Processing: Explorations in the microstructure of cognition. Vol. 1: Foundations (pp. 194-281). Cambridge, MA: MIT Press.

Smolensky, P. (1988). On the proper treatment of connectionism. Behavioral and Brain Sciences, 11, 1-74.

Thatcher, R. W., & John, E. R. (1977). Functional neuroscience vol. 1: Foundations of cognitive processes. Hillsdale, NJ: Erlbaum.

Thayer, H. S. (1973). Meaning and action. Indianapolis: Bobbs-Merrill.

Turner, C. D., & Bagnara, J. T. (1976). General endocrinology. Philadelphia: Saunders.

Tversky, A. (1977). Features of similarity. Psychological Review, 84, 327-352.

Tversky, A., & Gati, I. (1978). Studies of similarity. In E. Rosch & B. Lloyd (Eds.), Cognition and categorization. Hillsdale, NJ: Erlbaum.

van Gelder, T. (1992). What might cognition be if not computation? Cognitive Science Research Report #75. Indiana University, Bloomington, Indiana.

Vera, A. H., & Simon, H. A. (1993a). Situated action: A symbolic interpretation. Cognitive Science, 17(1), 7-48.

Vera, A. H., & Simon, H. A. (1993b). Situated action: Reply to William Clancey. Cognitive Science, 17(1), 117-133.

Vizi, E. S. (1984). Non-synaptic transmission between neurons: Modulation of neurochemical transmission. New York: Wiley.

Vizi, E. S. (1991). Nonsynaptic inhibitory signal transmission between axon terminals: Physiological and pharmacological evidence. In K. Fuxe & L. F. Agnati (Eds.), Volume transmission in the brain: Novel mechanisms for neural transmission. (pp. 89-96). New York: Raven.

Werner, H., & Kaplan, B. (1963). Symbol formation. New York: Wiley.

Winograd, T., & Flores, F. (1986). Understanding computers and cognition. Norwood, NJ: Ablex.

[1] Millikan (1984) proposes a model of representation in which correspondence per se is not so central. In many ways it is closer to the model we are outlining. Nevertheless, we argue elsewhere that it does not satisfy a crucial criterion for representation: that representational error be detectable by the representational system itself (see below, and Bickhard, 1993, in preparation-a, in preparation-b). Another candidate alternative, functional role semantics, has grave difficulties accounting for any kind of representational error, and cannot satisfy the requirement that error be detectable by the system itself (Bickhard & Terveen, 1995).

[2] A common and all too facile assumption is that the regress of interpreters is not vicious because it "bottoms out" in machine language -- in physically instantiated bit patterns. Machine language, so the assumption goes, just gets causally executed and doesn't have to be interpreted. Though what is claimed about machine language is correct as far as it goes, that gives no aid or comfort to the encoding position. Physically instantiated bit patterns in a computer are just a causal configuration of the machine (Hayes, Ford, & Adams-Webber, 1992); there are no representations at this causal machine level. But for "higher level" representationality to be cashed out in machine language terms requires an account of how representation for the machine emerges from this level of causal configurations. No such account is forthcoming. It is simply assumed that bit patterns inside the machine that correspond with things outside the machine, and thereby encode those external things. But whether representation can be reduced to correspondence is the very issue being debated (Newell, 1980; Vera & Simon, 1993a). Correspondence cannot be representation for the machine unless the machine can interpret the correspondence and recognize what is on the other end of it. The regress is still there, just as vicious as ever (see Bickhard & Terveen, 1995).

[3] The recent exchange between Vera and Simon (1993a; 1993b) and Clancey (1993) illustrates the mesmerizing hold that correspondence notions of representation can exert. Vera and Simon's commitment to a basic correspondence model is exemplified in statements like: "The case for regarding sensory inputs and motor outputs (whether of human or computer) as symbol structures is that they are patterns and they do denote. Being patterned and denoting are the two properties generally taken as defining symbols, and this is the definition that is used consistently in the literature associated with the physical symbol-system hypothesis" (Vera & Simon, 1993b, p. 123). This conception of representation stands or falls on its account of "denotation". Notwithstanding their continual criticisms of Clancey for failure to define his terms, Vera & Simon never attempt a definition of denotation. They never define the core of their purported model of representation.

In a small footnote (1993a, p. 12), they do allude to Putnam (1975) and Kripke (1972) as providing the needed theory of denotation. But Putnam has repudiated this earlier attempt (e.g., Putnam, 1990, 1992) and Kripke's model is a purely extensional endeavor which never attempted to characterize representation for the knowing agent (Block, 1986). Such carelessness about this central issue suggests that Vera and Simon take denotation to be unproblematic. In consequence, they are left with an empty conception of denotation, on which every single one of their further claims to be modeling cognition and representation rests.

This emptiness of their model of cognition is fully revealed in statements like: "The information in DNA and RNA is certainly represented symbolically, the symbols having clear denotations, but this information is not in the organism's conscious awareness" (Vera & Simon, 1993a, p. 44). If DNA and RNA are really symbols from their standpoint -- as would be perfectly appropriate given their conception of symbolism as covariant correspondence -- then their approach becomes utterly irrelevant to issues regarding cognition. If DNA contains denoting symbols, then why doesn't rain denote clouds? Why doesn't smoke denote fire? Why doesn't water trickling out of a snow bank denote the sun shining on the snow bank? Why don't activities inside a cell denote the transmitter molecule that docked on the cell surface and thereby triggered those internal processes? In every one of these cases we find covariation, and in some cases control, but in no case do we find representation. Vera and Simon seem ignorant of the issues involved here. They can retain their conception of symbol only if they are willing to give up any claim to be modeling anything like human cognition.

Their treatment of symbols says nothing about representational content, or intentionality, or "aboutness." It says nothing about a system or agent knowing anything about what is symbolized. Information in their sense of covariation is a legitimate concept, applicable to the design of various sorts of useful systems, but its relationship to cognition is unclear at best. As we have already established, conceptions of representation based on correspondence or covariation are incoherent (see also Bickhard & Terveen, 1995).

[4] This general point is complicated by issues involving the possibility of internal error, such as errors of efficiency or construction. These can be of major importance for some purposes, but they do not ultimately alter the general point, and we ignore them here.

[5] The claim that error must be error for the system is a claim about a requirement for naturalism. "For the system" is meant in the sense of functionally accessible to the system, and is in contrast with models that attempt to model representational error, but do so in ways that could only be assessed, and, thus, only accessed, by an external observer of the system. Error that is dependent on an external observer is not error "for the system". Such error could not be functionally accessed by the system, and, therefore, error guided processes, such as error guided interaction or error guided learning, would be impossible. (This functional notion of "for the system" does not require awareness or representation of that error -- at least not so long as the functional accessibility and assessability can be modeled without such awareness or representation.)

Contemporary models of representation and representational error violate this naturalistic requirement. Representational error assessment in these models requires prior assessment of evolutionary or learning history, or of counterfactual symmetries and asymmetries of dependencies between correct and errorful instances of "representation" (Dretske, 1981, 1988; Fodor, 1987, 1990; Millikan, 1984, 1993). In none of these models could a frog, for example, have error for the frog because the frog cannot undertake any such assessments (Bickhard, 1993, in preparation-a, in preparation-b; Bickhard & Terveen, 1995).

The model of representational error presented in the text is dependent on an underlying model of function and functional error. That model of function must also be adequate to functional error for the system in order for representational error to be for the system. For discussions of such a model of function, see Bickhard, 1993, in preparation-a, in preparation-b; Christensen, in press, in preparation.

[6] There is a slightly subtle possibility here. Suppose a system already wants a certain result (has an internally specified goal to this effect), but cannot bring it about. Then the part of the system that determines whether the current trial result is correct could serve as the error feedback generator for the part of the system that is generating trials toward the sought-for result. In this case, the trial generator must emit its trials to the error feedback generator, so again it is not passive. Note, too, that such "learning" is limited to whatever predesigned criteria for error that the system may already contain.

[7] Systems with no output can certainly change, and such changes might be taken as capturing something about the inputs -- something about their statistical properties, for instance. This might be construed as a form of learning, but everything in the design of the system that leads it to make specific internal changes in response to inputs has to be built into that system before it processes any of those inputs. No learning can occur at this level of system design; there is no way for the system to modify the internal changes that it is capable of. Such a passive system might be capable of selections among predesigned alternative internal responses to inputs. It will not be capable of anything beyond those predesigned alternatives.

[8] Note that a correspondence -- an encoding -- could not be taken to be in error by the system. The system has no information about what might be on the other end of any such correspondence, and, therefore, cannot change it. The system can have functional access to information about the inputs induced by certain of its outputs (or the interaction trajectories made possible or prohibited by other interaction trajectories), but it does not have access to what its inputs are in correspondence with. Access to the other end of such correspondences would have to be epistemic, not functional, yet epistemic access is precisely what is at issue.

[9] microgenetically! See below.

[10] In this discussion, we have tried to avoid getting ahead of ourselves; we have presumed that error is all or nothing. That is, particular expectations about the input consequences of producing a particular output are either true or false; there are no gradations of success and failure. The all-or-none conception is appropriate so long as we consider system states to be discrete and not topologically organized.

But if the space in which different system states are indicated has a topology of its own, some errors or failures will be bigger than others. Indeed, in a metric space, misses can be at varying distances from the goal state. Error that is graded in such a fashion can provided additional information for error-guided processes. (See below.)

[11] Unlike encodings, which are representations precisely because they represent their truth conditions: "There is a dog" is true if and only if there is a dog on the other end of the correspondence.

[12] These arguments are intended to motivate and introduce the interactive model. There are many other arguments in favor of interactivism, and arguments against encodingism (Bickhard, 1993; Bickhard & Terveen, 1995). There are also other candidate models of representation that we do not address here -- though we argue elsewhere that they all are vulnerable to similar criticisms. None of them, for example, can satisfy the need for system-detectable error. See Bickhard (1993, in preparation-a) and Bickhard & Terveen (1995) for more extensive arguments and considerations of a wider range of candidate alternatives.

[13] This is an interactive version of what is called "recognition" or "acceptance" in abstract machine theory (Eilenberg, 1974; Ginzburg, 1968; Hopcroft & Ullman, 1979). In the interactive version, outputs can induce inputs, via the environment, so it is not merely input strings that are passively "recognized". Elaborations of more formal perspectives on the interactive model can be found in Bickhard, 1980, 1982, 1993; Bickhard & Campbell, 1992; Bickhard & Terveen, 1995; Campbell & Bickhard, 1992a.

[14] For our purposes, it makes no difference whether we are presumed to be born with representational indentations in our wax, or the indentations are made exclusively after birth. Encoding-based nativism (e.g., Fodor, 1975, 1981a) makes the same objectionable assumptions about representation that empiricism does.

[15] For some extensive investigations of such oscillatory and modulatory phenomena in crustacean stomatogastric nervous systems, see Harris-Warrick, Marder, Selverston, and Moulins, 1992. As Sahley (1993) points out, "These concepts are certain to be of ever greater significance as more complex systems and their behaviors are investigated."

[16] As Hanlon (1991b) points out, there is a long tradition of microgenetic perspectives in the neurosciences (Brown, 1988; Deacon, 1989; Hanlon, 1991a). In fact, such ideas considerably predate Werner's formulations. Interactivism has strong convergences with this tradition on certain issues -- see, for instance, Hanlon's (1991b) point that the "dynamic states" of the brain that underlie cognition must take the form of wave fronts, or Schweiger's (1991) incorporation of Piagetian themes. Other features of this tradition -- its strict holism and recapitulationism -- are less consistent with our conceptions. The history of thinking about microgenesis, and the difference between old and new conceptions (Catán, 1986; Hanlon, 1991b), are topics that deserve serious examination in a different forum.

[17] Such topological information is not necessary for completely blind variation and selection. It is a requirement for heuristic problem solving; such heuristics can't be architecturally realized without it.

[18] We will discuss some deeper and more evolved aspects of Gentner's theory below, after we have presented enough of the interactive framework to be able to make more detailed comparisons. It turns out that, in spite of the fundamental differences between information processing and interactivism, there is a strong convergence between a number of characteristics of Gentner's model and characteristics that are intrinsic to the interactive model.

[19] This claim is "roughly" correct, but it slides over some basic distinctions between stand-in relationships among external elements, and stand-ins among conditions in the mind. Briefly, external elements and their encoding relationships must both be interpreted, while encoding relationships in the mind cannot require such interpretation on pain of an infinite regress of interpreters. See Bickhard and Richie (1983) for a discussion of internal stand-ins.

[20] Which of those continuous maps to manifest -- which processes of comparison to use -- can, of course, be a significant problem, as can discovering and constructing a space of possible such maps (Medin, Goldstone, & Gentner, 1993). The processes that manifest such maps must themselves be learned and constructed, and will form a domain or field of individual development (Gentner, 1988; Gentner & Rattermann, 1991 -- though we are not in agreement with their characterization of that development: Bickhard, 1992b, 1992c; Campbell & Bickhard, 1986). Such processes are also subject to historical discovery and development (Bickhard, 1991c; Gentner & Grudin, 1985; Gentner & Jeziorski, 1993). Note also that given a domain and a continuous map, they can be used to conjecturally fill out the codomain of the map: given a space of comparison and a method of comparison, analogy and related processes can speculate about properties and structures of the target domain. For more on these points, see the discussion of "Analogy and Similarity, Again" in the main text below.

[21] For example, the problem solving tradition of Newell and Simon, culminating in the SOAR architecture, permits only generalizations with regard to predefined variables that are involved in the definitions of the problem states (Bickhard & Terveen, 1995). Not only are the dimensions of generalization predefined, there is no such thing as generalization of the procedures; it is not even clear what that could mean within standard information-processing architectures.

[22] Note that the combinatoric constructions of problem or solution or model representations involved in some expert systems (Clancey, 1992) will generate a topology in that representational space. We know of no sophisticated use of that topological information, however. More fundamentally, these spaces are 1) strictly combinatoric in their constructive power, and 2) would not exist at all unless their "atoms" were predefined and preprogrammed. Standard expert system approaches cannot explain the origin of representational spaces.

[23] One interesting example of interaction among these facets of microgenetic activity is the re-representation of representational domains. This involves modification of the microgenetic processes involved so as to increase similarity between the domains (that is, alter their microgenetic topologies so that continuous maps between them more easily or fruitfully defined -- Gentner & Markman, 1995). In such cases, the success (or failure) of the microgenetic processes in supporting representational comparisons functions as a selection constraint on variations of those microgenetic processes.

[24] The inheritance organizations in object-oriented programming are an example of explicit constructive topologies that are made available to a programmer as a resource (Goldberg & Robson, 1983; Pascoe, 1986). Such programmer's topologies illustrate both how useful, even necessary, such topologies can be, and how difficult and complex their construction can be. It is of interest that the evolution of programming has focused more and more on such constructive resources and their topologies: macros, subroutines, modules, objects, agents, and so on.

[25] One possible ground for such variation and selection is the selective enhancement and pruning of neural modulatory connections (Edelman, 1987, 1992; Reeke & Edelman, 1988). Patterns of selective differentiation constitute alterations in the overall modulatory influences that can be microgenetically constructed in the corresponding local domains of the nervous system. That is, alterations in the patterning of the physical basis for modulation will constitute alterations in the modulatory relationships that will be microgenetically constructed -- even if the microgenetic constructive process is not altered at the biochemical level.

[26] Provided, of course, that the system is capable of modifying itself. A system that is capable of knowing, but not of learning, will not be microgenetically flexible in this way.

[27] A causal theory of names would seem to sidestep this problem. But it does so by presenting strictly externalist criteria for naming relationships, while failing to explain how a knowing agent could have names and make use of them (see footnote 3). A successful naturalistic account of representation cannot sidestep such issues about representational agents.

[28] In a striking and exciting convergence with the interactivist emphasis on microgenesis, however, recent work bases the computation of proportional analogy problems on the steps by which the items to be compared are constructed (Hofstadter, 1995; O'Hara, 1994; O'Hara & Indurkhya, 1995). As is by now familiar, however, these models allow only constructions using a pre-designed set of constructive rules and a fixed set of atoms as building blocks.