PRL online - Relevant Issue, 82(1) - This paper
Non-Local Contributions to Degenerate Four Wave Mixing in Noncentrosymmetric Materials
Ivan Biaggio
Nonlinear Optics Laboratory, Institute of Quantum Electronics,
Swiss Federal Institute of Technology, ETH-Hönggerberg,
CH-8093 Zürich, Switzerland
(Received 11 September 1998)
|
Cascaded second order and piezoelectric contributions to degenerate four wave mixing in non-centrosymmetric materials are analyzed in detail. The effective third order susceptibility measured in degenerate four-wave mixing becomes strongly dependent on experimental parameters that do not normally influence the third order response in centrosymmetric materials. This introduces new important requirements for a reliable reporting of experimental results. A new technique that allows to experimentally relate the third order susceptibility to the high-frequency electro-optic and dielectric properties is introduced and demonstrated in BaTiO3 and KNbO3. PACS Numbers: 78.20.Bh, 42.65.Hw, 77.65.-j, 77.84.-s |
Pulsed Degenerate Four Wave Mixing (DFWM) is a wide-spread tool for characterizing third order susceptibilities of candidate materials for nonlinear optical applications. We discuss important second order effects that cause unexpected geometrical and pulse-length dependencies of the DFWM signal. They are due to the concurrent processes of optical rectification and linear electro-optic effect, and to piezoelectric elastic relaxation. If neglected, these "cascaded" second order effects can lead to misleading DFWM results in non-centrosymmetric materials. In this work we give the first complete expressions to calculate their contributions to the DFWM signal, and show how they can be used to relate experimentally the third order susceptibility to the linear electro-optic and dielectric properties.
We first point out the origin of second order contributions and give general equations for calculating them for the most important DFWM set-ups, correcting and completing some expressions given in Ref. 1. We then discuss the piezoelectric relaxation of the crystal as it is constrained by the boundary conditions defined by the DFWM experimental geometry, and calculate the effective electro-optic and dielectric tensors to be used when relaxation to a new elastic configuration is possible. Lastly, we demonstrate experimentally, in the well known electro-optic materials BaTiO3 and KNbO3, how these results can be used to obtain absolute third order susceptibilities by comparing to independently determined electro-optic and dielectric properties, without using a reference material.
We start with the definition of the third order nonlinear optical susceptibilities. Consider an electric field that is a sum of three plane waves with wave vectors ki and frequency w:
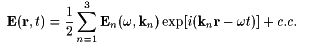 |
(1) |
The field of (1) induces a time-dependent third order polarization [2,3]:
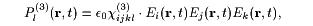 |
(2) |
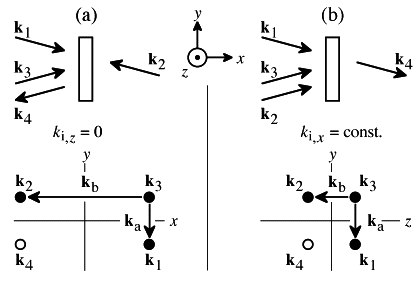
Figure 1 shows two ways of arranging the three input waves so that the nonlinear polarization at frequency w and wavevector k4=k1 + k2 - k3, with complex amplitude P(w,k4), radiates the signal wave in a phase matched way over the whole sample thickness. Inserting (1) into (2), and collecting the terms with frequency w and wavevector k4, one finds:
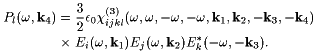 |
(3) |
| Figure 1: Two common DFWM experimental geometries. Three beams with wavevectors k1, k2, and k3 interact in a sample to generate a fourth beam with wavevector k4. The interacting beams and the sample are drawn in the x-y plane in the first line, and the coordinates of the beam wavevectors are plotted in the second line. For clarity, the x and y axes are not in scale. (a) Beams 1 and 2, and beams 4 (signal) and 3, are counterpropagating [3]. (b) All input input beams travel towards the positive x direction. The beams are distinguished by a slightly different z direction [11]. |
Our S.I. expressions use the same convention as in Ref. 4. They go over to the ones in electro-static units (e.s.u.) of Refs. 2,3, used in a relevant part of the literature, with the substitution ![]() , while numerical values are converted using the rule
, while numerical values are converted using the rule
 |
(4) |
In a noncentrosymmetric material, the field of (1) also leads to a second order polarization. The only part that gives a large phase matched contribution to DFWM is induced by optical rectification, and it consists of the sum of two components oscillating in space like a plane wave. Their complex amplitudes are
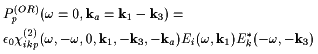 |
(5) |
 |
(6) |
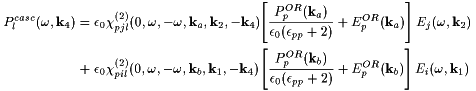 |
(7) |
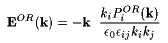 |
(8) |
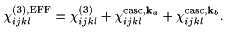 |
(9) |
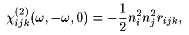 |
(10) |
We can now write ccasc, kaijkl and ccasc, kbijkl for ka and kb parallel to a main axis of the dielectric tensor. For P(OR)(w=0,k) perpendicular k (transversal polarization):
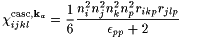 |
(11) |
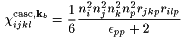 |
(12) |
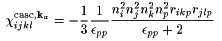 |
(13) |
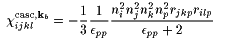 |
(14) |
In (11)-(14), rijk and eij are electro-optic and dielectric tensors at constant strain when short enough pulses are used, but they are effective tensors including acoustic phonon contributions when the spatial periods 2p/ka or 2p/kb are so small that elastic deformations can build up during the laser pulse length. This can already be the case for 100 ps pulses for one of the contributions of Fig.1a: 2p/kb can reach 0.1 µm inside the crystal for a light wavelength of ~0.5 µm, and an acoustic wave with a speed of 5 km/s travels that distance in 20 ps.
These effective tensors are not simply the directly measurable ones at constant stress (unclamped) because only certain acoustic phonon contributions are allowed. The electric and strain fields in the crystal must have in our case a plane-wave spatial dependence E(k)= E exp(i k x) and u(k)= u exp(i k x) with the complex (vectorial) amplitudes E and u. This boundary condition breaks the symmetry of the crystal, leading to modified, wavevector dependent rijk and eij tensors with a lower symmetry. A similar problem has been treated in Ref. 6 assuming an electric field always parallel to the modulation wavevector. In our case the rectified polarization can also be perpendicular to the wavevectors ka and kb and we need to treat the problem in general by looking at the general relationships between electric field, strain, and dielectric tensor. The electro-optic tensor rSijk at constant strain and the elasto-optic tensor pEijkl at constant electric field determine the change in the dielectric tensor induced by the spatially sinusoidal electric and strain fields:
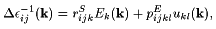 |
(15) |
By calculating u(k) from E(k), we can relate the amplitude of the dielectric tensor modulation (15) to the amplitude of the electric field modulation E with an effective electro-optic tensor rijk defined by D e-1ij= rijkEk.
The stress tensor Tij can be expressed as a function of the strain tensor Skl=(ukl+ulk)/2 and the electric field by means of the elastic stiffness tensor at constant electric field CEijkl and the piezoelectric tensor eijk:
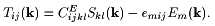 |
(16) |
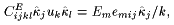 |
(17) |
Defining ![]() and
and ![]() , and substituting in (17), reveals the system of three linear inhomogenous equations Aik uk = bi. The matrix Aik is symmetric and can be inverted [7] to obtain the solution uk=Aki-1bi, which is then inserted in (15) to get the effective electro-optic coefficient we were looking for:
, and substituting in (17), reveals the system of three linear inhomogenous equations Aik uk = bi. The matrix Aik is symmetric and can be inverted [7] to obtain the solution uk=Aki-1bi, which is then inserted in (15) to get the effective electro-optic coefficient we were looking for:
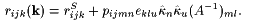 |
(18) |
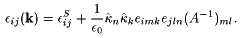 |
(19) |
In centrosymmetric materials, any coefficient c(3)ijkl defined in (3) can be measured in DFWM by appropriately choosing the polarizations of the 3 input beams and the signal beam in the sample reference-frame.
This is not true for non-centrosymmetric materials. Even when the polarizations are kept constant in the sample reference-frame, the second order non-local contributions depend on the wavevector differences ka and kb, and change with sample orientation, DFWM set-up, and pulse-length.
To fix the ideas, we calculate the influence of these parameters for tetragonal BaTiO3 and orthorhombic KNbO3. We use the rSijk extrapolated at 1.06 µm [8], and Refs. 6 and 9 for the other material constants.
The separate contributions from POR(ka) and POR(kb) are shown in Table 1 for the two DFWM geometries of Fig.1 and two orientations of the polar 3-axis of the crystals (labelled c). All light polarizations are kept constant in the sample reference-frame and the direct third order contributions do not change with crystal orientation or experimental set up. The cascaded contributions, on the other hand, vary considerably. As an example, c(3)3333 can be measured with (i) c parallel y and all beams polarized along y, or (ii) c parallel z and all beams polarized along z (the angles between the beams can always be chosen so small that the x-components of the optical electric field are negligible). For c(3)3333 only r333 contributes to POR, which is then parallel to c. For the set-up in Fig.1a, both rectified polarizations are transversal for c parallel z, while POR(ka) becomes longitudinal for c parallel y. For the Fig.1b set-up, POR(ka) is transversal and POR(kb) longitudinal for c parallel z, and vice-versa for c parallel y. To give an example of its effect, we include piezoelectric elastic relaxation for the contribution with the large wavevector kb in Fig.1a. All other cascaded contributions were calculated using the clamped (strain-free) coefficients, and are valid up to laser pulse lengths of several nanoseconds, depending on the angle between the beams. The same reasoning can be applied to c(3)1133 and c(3)2233, but here the piezoelectric contribution for ka,b perpendicular c always vanishes by symmetry, as can be demonstrated with (18).

Despite the fact that direct third order contributions are identical for every pair of rows of Table 1, the total cascaded contributions can differ by a factor of ~ 2. They are different for the two experimental set-ups of Fig.1 and change with sample orientation in the set-up of Fig.1a. Interestingly, in the set-up of Fig.1b, the total cascaded contribution does not depend on the orientation of the sample. Note also that, in the set-up of Fig.1a, acoustic phonons contribute about 50 % to c(3), EFF3333 (c parallel y) of KNbO3 (which corresponds to more than a factor of 2 for the DFWM signal).
The total energy in the signal pulse in DFWM is ![]() , where z is an unknown calibration factor that depends on difficult to control parameters such as beam profiles and overlap in the sample, h collects all known experimental quantities that affect the measurement, and c(3), EFF is the active effective susceptibility coefficient.
, where z is an unknown calibration factor that depends on difficult to control parameters such as beam profiles and overlap in the sample, h collects all known experimental quantities that affect the measurement, and c(3), EFF is the active effective susceptibility coefficient.
For noncentrosymmetric materials the geometry dependencies showcased in Table 1 can be exploited, in place of a reference material with well known susceptibility, to determine the calibration factor z:
 |
(20) |
We applied this technique in the experimental geometry of Fig.1a for BaTiO3 and KNbO3. The measurements were performed using c(3)2233 for the calibration and comparing the other coefficients to the c(3)2233 set-up by taking into account the different light beam polarizations. c(3)2233 was chosen because of its large cascaded contributions and the absence of piezoelectric relaxation (rijk=rSijk), which minimizes the influence of experimental errors and the number of material parameters that must be known.
The experimental susceptibilties values we measured at 1.06 µm and for 100 ps pulses are, in units of 10-22 m2/V2, c(3) EFF1133(c parallel y)=560± 80, c(3) EFF1133(c parallel z)=340± 80 for BaTiO3, and c(3) EFF2233(c parallel y)=330 ± 70, c(3) EFF2233(c parallel z)=190 ± 50 for KNbO3. Note that the direct third order contributions are only c(3)1133 ~ 110 for BaTiO3 and c(3)2233 ~ 60 for KNbO3. For the other coefficients, c(3)1111~ 160, c(3)3333 ~ 100 for BaTiO3, and c(3)2222 ~ 180, c(3)3333 ~ 60 for KNbO3. A more detailed discussion of these experimental results will be given elsewhere.
The results above where checked with a classical reference measurement. Comparing the experimental signal to the one observed with a 1 mm thick cell filled with CS2, and using c(3) CS21111 =263 ± 30 [10], we got c(3)1133(c parallel y)=550 ± 100 for BaTiO3 and c(3)2233(c parallel y)=290 ± 60 for KNbO3.
This is in excellent agreement with the results obtained above using the cascading contributions in Table 1 as a reference, confirming the validity of the expressions and theoretical interpretations given in this paper.
In conclusion, we have demonstrated that DFWM in non-centrosymmetric materials requires special care in selecting experimental geometries in order to deliver reliable results, and we have shown how to calculate the geometry dependent second order contributions for different pulse lengths. The second order contributions can be exploited to calibrate a DFWM experiment and relate third order susceptibilities to second order dielectric and electro-optic properties experimentally.
References
- M. Zgonik and P. Günter, J. Opt. Soc. Am. B 13, 570-576 (1996).
- P. D. Maker, R. W. Terhune, Phys. Rev. 137, A801-A818 (1964).
- R. W. Hellwarth, Prog. Quant. Electr. 5, 1-68 (1977).
- R. W. Hellwarth, J. Opt. Soc. Am 67,1 (1977).
- P. N. Butcher, D. Cotter, "The elements of nonlinear optics," Cambridge University Press 1991.
- F. P. Strohkendl, L. R. Dalton, R. W. Hellwarth, H. W. Sarkas, Z. H. Kafafi, J. Opt. Soc. Am. 14, 92 (1997).
- Chr. Flytzanis, N. Bloembergen, Prog. Quant. Electr. 4, 271-300 (1977).
- M. Zgonik, R. Schlesser, I. Biaggio, E. Voit, J. Tscherry, P. Günter, J. Appl. Phys. 74, 1287 (1993).
- F. I. Fedorov, "Theory of elastic waves in crystals," Plenum Press, New York 1968.
- P. Bernasconi, M. Zgonik and P. Günter, J. Appl. Phys. 78, 2651 (1995).
- M. Zgonik, P. Bernasconi, M. Duelli, R. Schlesser, P. Günter, M. H. Garret, D. Rytz, Y. Zhu, X. Wu, Phys. Rev. B 50, 5941-5949 (1994).
- N. Tang, J. P. Partanen, R. W. Hellwarth, R. J. Knize, Phys. Rev. B 48, 8404 (1993).