Elementary
Statistics.
An
example on Standard Deviation:
Given a set of data we know how to locate the maximum value, the minimum value and the arithmetic mean. We have seen several examples and the methods can be summarized as follows:
For the maximum, we designate as temporary maximum the first element of the data and then we sweep through the rest one by one. As we do so, we compare each entry to the temporary maximum. If the current entry is greater than the temporary maximum then we replace the temporary maximum by this entry, otherwise we pass. At the end the temporary maximum will end up being the actual maximum.
For the minimum we follow the exact same procedure but of course we replace the temporary minimum with the current entry only if the entry is less than the temporary minimum.
For the arithmetic mean we form the sum of all data using sum = sum + entry and then at the end we divide the sum by the number of entries.
Another elementary statistical characteristic of a given set of data is the Standard Deviation. Look at the two sets of data given below
|
67 |
65 |
66 |
68 |
69 |
64 |
62 |
|
|
|
|
|
|
|
|
|
90 |
71 |
60 |
50 |
40 |
60 |
90 |
Both have arithmetic mean 65.86 but they are different in character. In the first set all numbers are near and about 65 or 66. But in the second set the max is 90 and the min 40. How can we quantify the difference between the two sets? We can calculate the standard deviation using the formula:
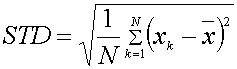
Here x with a bar denotes the arithmetic mean ( 65.86 for the present examples) and N is the number of data entries ( 7 in these examples). Calculation of STD using our calculator produces 2.23 for the first set but 17.65 for the second set.
Using arrays makes the calculation of STD very simple. Here we give an example program which performs such a calculation
/* An example on the use of arrays :
Calculating the standard deviation in a
list of scores in a data file.
file: 6ex4.cpp
FALL 1998
___________________________________
Jacob Y. Kazakia jyk0
October 13, 1998
Example 4 of week 6
Recitation Instructor: J.Y.Kazakia
Recitation Section 01
___________________________________
Purpose: This program reads a column of 20
float numbers from a file
named 6ex4data.txt into the array a[20] .
It outputs these numbers to a
file named 6ex1rep.txt .
It then outputs to the same file the average score and the
standard deviation.
Algorithm: The average score avg is obtained
by calculating the sum of
the twenty scores and then dividing by 20.
For the standard deviation we first calculate the sum of the
squares of score - average
score, ie.
sumsq = sum ( from m=0 to m=19) of { (a[m] - avg ) ^ 2 },
and then we calculate the standard deviation std by:
std = sqrt ( sumsq / 20 )
*/
#include <iostream.h>
#include <iomanip.h>
#include <fstream.h>
#include <math.h>
void main()
{
// declare the variables of the main
function
float a[20]; // This is an array of
twenty entries named as:
// a[0],
a[1], a[2], ......., a[18], a[19].
int m;
float sum = 0.0;
float avg = 0.0; // the average score
float sumsq = 0.0 ;
float std = 0.0;
ifstream FinalExam ( "6ex4data.txt" , ios:: in);
ofstream report ( "6ex4rep.txt" , ios:: out);
for ( m = 0 ; m <= 19 ; m++ )
{
FinalExam >> a[m] ;
report << setiosflags( ios :: fixed) <<
setprecision(1);
report << "
a( " << setw(2) << m <<" ) = "<<
setw(5) << a[m];
sum = sum + a[m] ;
report << endl;
}
// calculation of the average
avg = sum / 20 ;
report << setprecision(4);
report <<"\n\n the average score is: " << avg
<< endl <<endl;
// calculation of the standard deviation
for ( m = 0 ; m <= 19 ; m++ )
sumsq = sumsq + ( a[m] - avg )* ( a[m] - avg );
std = sqrt ( sumsq / 20 );
report << " \n\n The standard deviation is: " << std << endl
<< endl ;
cout<< " \n\n
DONE ! The output is in the file 6ex4rep.txt \n\n";
cout<<" \n\n enter e (exit) to
terminate the program....";
char hold;
cin>>hold;
}
/*
THIS IS THE FILE 6ex4rep.txt :
a( 0 ) = 78.5
a( 1 ) = 67.3
a( 2 ) = 90.9
a( 3 ) = 89.6
a( 4 ) = 23.4
a( 5 ) = 0.0
a( 6 ) = 67.5
a( 7 ) = 89.6
a( 8 ) = 79.5
a( 9 ) = 77.3
a( 10 ) = 94.9
a( 11 ) = 89.6
a( 12 ) = 45.4
a( 13 ) = 10.0
a( 14 ) = 67.5
a( 15 ) = 89.6
a( 16 ) = 78.5
a( 17 ) = 67.3
a( 18 ) = 90.9
a( 19 ) = 89.6
the average score is: 69.3450
The standard deviation is:
27.3840
*/
( Click here
for a text file of the above example 6ex4 )
© 2001 J. Y. Kazakia All rights reserved