On-line Math 21

On-line Math 21

5.1  The definition of the Riemann Integral

Example 4 Show that
ó
õ 		2p

0 
 sin2xdx = p.
The same is true for cos2x ,
ó
õ 		2p

0 
 cos2xdx = p.

Solution

This is a classic integral. It is not only one of the few trigonometric integrals that can be solved with absolutely no techniques of integration, but it is one of the most useful. In later courses, you will run across these two integrals, and simple variations of them, over and over again. To be able to evaluate those integrals on sight saves a lot of headaches.

There is a way to solve these integrals using techniques of integration, but that is more than you need to do here. This method specifically will work for integrals over a full period of the function, not for more general intervals.

First, graph y = sin2(x) over that interval.

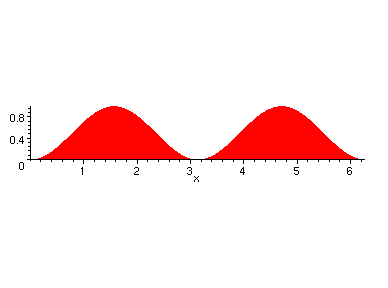Note that this graph is basically two ``hills''. Both are above the axis since sin2(x) is of course always positive. Now compare that graph to that of cos2(x) over the same interval,

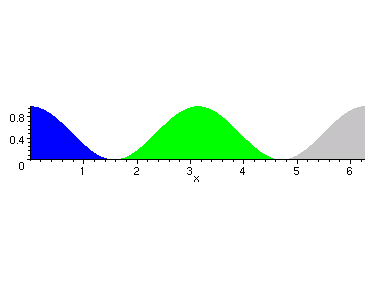Notice that the different-colored areas of this graph can be put into correspondence with those of sin2(x) , so that
ó
õ 		2p

0 
 sin2(x)dx = ó
õ 		2p

0 
 cos2(x)dx.
On the other hand, since
sin2(x)+cos2(x) = 1
at each point (the basic trigonometric identity),
ó
õ 		2p

0 
 sin2(x)dx+ ó
õ 		2p

0 
 cos2(x)dx
=
ó
õ 		2p

0 
 ( sin2(x)+cos2(x)) dx
=
ó
õ 		2p

0 
 1 dx
=
2p.
Since the two integrals are the same, and the sum of the two comes up to 2p, each one must be half that, p, that is,
ó
õ 		2p

0 
 sin2(x)dx = p = ó
õ 		2p

0 
 cos2(x)dx.
There are several similar integrals to these, the most general being:


ó
õ 		a+np

a 
 sin2(kx)dx = np
2
 = ó
õ 		a+np

a 
 cos2(kx)dx,
where a is any number, but n and k have to be integers, with n positive. The proof is exactly the same, but you do have to be a bit careful to make sure you have the right pieces to make it work.

Copyright (c) 2000 by David L. Johnson.

File translated from TEX by TTH, version 2.61.
On 29 Dec 2000, 22:58.