On-line Math 21
On-line Math 21
5.1 The definition of the Riemann Integral
Example 1
If
then
Solution
Here is the graph:
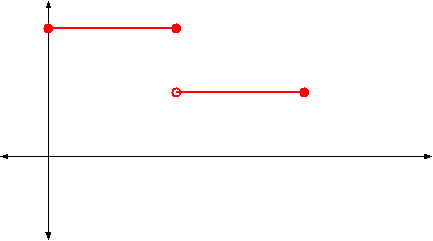Since this function is just a constant over the two halves of the interval,
if we were lucky enough that the subdivision had a division at x = 1 ,
we would have that the first part of the Riemann sum would be just the height
(1) times the total width (also 1). If we were even luckier, for that first
interval past x = 1 , the xi* sampling point would not
have been chosen to be at x = 1 , and the height would be 1/2 for all those
subintervals, so that the part of the sum past x = 1 would have value (1/2)·1 = 1/2 .
Under those lucky circumstances, the Riemann sum would total
which is what we want.
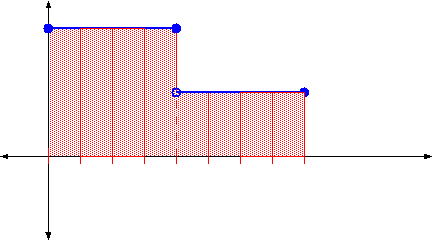But, even if we aren't so lucky, the only thing that would get messed up is
one subinterval; if the subdividing point does not exactly hit at x = 1 ,
or if it does, but we were unlucky enough to have chosen the left-hand edge
as the sampling point, then only one rectangle would not fit so neatly. In general,
the situation might look like this:
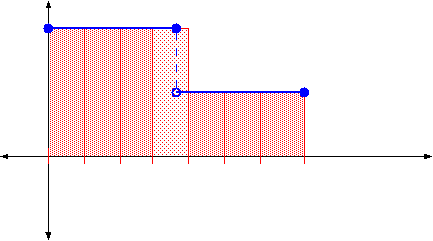That one ``bad'' rectangle covers a bit more area than the area under
the curve, and so the Riemann sum would overstate the total area. On the other
hand, if the sampling point were for an xi* > 1 , then, instead, the
area would have been too small. But the total amount of missed area can't be
any larger than the size of that one rectangle. so
|
3/2-1·||P|| £ |
n
å
i = 1
|
f(xi*)Dxi £ 3/2+1·||P||, |
|
where ||P|| is the mesh of the partition, the width
of the largest subinterval, (which is probably bigger than the one problem subinterval).
Clearly, as that mesh goes down to 0, the error must also disappear, and
Copyright (c) 2000 by David L. Johnson.
File translated from
TEX
by
TTH,
version 2.61.
On 29 Dec 2000, 22:48.