On-line Math 21

4.3 Max-min problems

Example 1 A cardboard box

Find the dimensions of the largest cardboard box with a square base which uses only 12 square feet of cardboard. For a cardboard box, remember that the top and bottom have two layers of cardboard (for the flaps), while the sides are a single layer.

Remark 2 This is typical of real problems, in that the problem is poorly phrased. Largest how? Largest in volume.

Solution

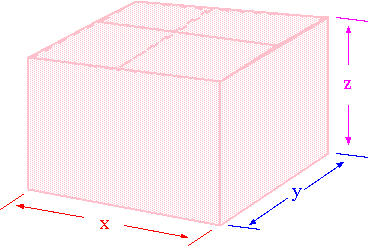
Begin by drawing a sketch of the box, and then label the sides which might vary, as say x , y , and z , where z is the height.

We have to maximize the volume V = xyz . But, there are in this example 2 constraints, to get us down to a function of one variable. The simpler constraint is that x = y , since the base is square. The other is in terms of the amount of cardboard to be used. If S is the amount of cardboard,

S = 4xy+2xz+2yx = 4x²+4xz,

where the fact that the top and bottom have a double layer is included in the 4xy term, and the right and left sides, and front and back, account for the other terms. The last equation comes from setting y = x .

Now, you are given that S = 12 , so

12 = 4x²+4xz,

or, solving for z , z = (3-x²)/x = 3/x-x . Also from that constraint comes the fact that 0 Ł x Ł Ö3 . x is a physical length, so can't be negative, and x Ł Ö3 since, if x > Ö3 , the area of cardboard required just for the flaps would be larger than the amount alloted.

Substitute these constraints in the original thing we wanted to optimize, and

V = xyz = xx(3/x-x) = 3x-x³ = f(x)

is the function you have to maximize. Differentiate f , and set it to 0, and:

0 = f˘(x) = 3-3x²,

so x = 1 . Not ą1 , since -1 is not a physical length.

This value of x , x = 1 , is the place where the maximum occurs. Why? Because the only place where there can be a maximum is where the derivative is 0, where the derivative doesn't exist, or the endpoints. Also, if there are endpoints of the interval that make even halfway sense, there must be a maximum. In this case the endpoints, x = 0 and x = 3 , both give V = 0 . So, x = 1 , giving V = 2 , must be the maximum. You find out which of the possible points is the optimum you want by evaluating the function at all the possible points.

By the way, you then should re-read the question to find out what is asked for. In this case, it asks for the dimensions of the box: x = y = 1 you already have. You then solve for z , using the constraint, z = 3/1-1 = 2 .

File translated from T_EX by T_TH, version 2.61.
On 8 Dec 2000, 00:23.