On-line Math 21

4.5  Curve Sketching

Example 7

y = Öx-   ___ Öx-1   .

Solution

   Asymptotes

Here there are no vertical asymptotes, even though there is an ``end'' to the domain. This function is only defined for x ³ 1 , so that the stuff inside the square roots is always positive.

Now, for horizontal asymptotes,

lim x® ¥  Öx-   ___ Öx-1   = lim x® ¥  æ è Öx-   ___ Öx-1   ö ø æ è Öx+   ___ Öx-1   ö ø æ è Öx+   ___ Öx-1   ö ø = lim x® ¥  ( x-(x-1)) æ è Öx+   ___ Öx-1   ö ø = lim x® ¥  1 æ è Öx+   ___ Öx-1   ö ø = 0,

so the x -axis is a horizontal asymptote. Since f(x) > 0 , the tail is above the horizontal asymptote on the right (there is only the asymptote on the right).

   Intercepts

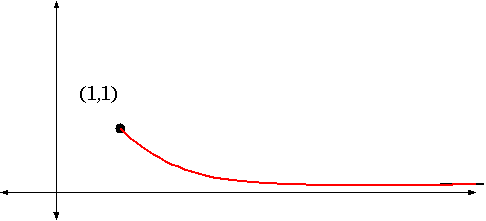
Here we should also worry about endpoints. Since x ³ 1 is the domain, we need to find f(1) , which is of course 1 . The only place to look for intercepts is on the x -axis, which requires a solution of

0 = f(x) = Öx-   ___ Öx-1   , or Öx =   ___ Öx-1   ,

which has no solutions. So there are no intercepts.

   Increasing/decreasing, and critical points

f¢(x) = 1 2Öx - 1 2   ___ Öx-1   =   ___ Öx-1   -Öx 2Öx   ___ Öx-1   ,

so, just as there were no x -intercepts, there can't be any critical points. f¢(x) < 0 for all x.

   Concavity, and inflection points

f¢¢(x) = æ ç ç ç è 1 2Öx - 1 2   ___ Öx-1   ö ÷ ÷ ÷ ø ¢ = æ ç è 1 2 x-1/2- 1 2 (x-1)-1/2 ö ÷ ø ¢ = - 1 4 x-3/2+ 1 4 (x-1)-3/2 = x3/2-(x-1)3/2 4x3/2(x-1)3/2 ,

which is always positive. So, there are no inflection points, and the graph is always concave up.

   Draw the graph

Use this information to draw a fair representation of the graph.

• The first information you plot are the asymptotes and ``tails'' [Link to ex7-1.gif]
• Then find intercepts and endpoints; [Link to ex7-2.gif]
• Then plot the critical points (and values). Again, none in this case.
• Plot the inflection points. Also none of these.
• Then fill in the graph, connecting the dots and making sure that the graph you draw is increasing/decreasing where the number line indicates it should be, and concave-up or concave-down where the sign of the second derivative indicates. [Link to ex7-3.gif]

[Each of these items should trigger the appearance of a new drawing with that information added.]

Copyright (c) 2000 by David L. Johnson.