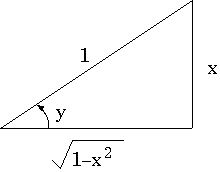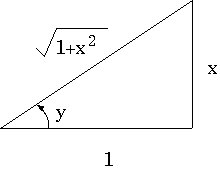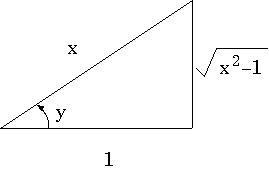On-line Math 21
On-line Math 21
3.1 Trigonometric functions
3.1.4 Derivatives of inverse trig functions
Inverse Trigonometric Functions.
For someone uncomfortable with trigonometric functions and all their identities,
the thought of having to worry about inverse-trigonometric functions
may be a little unnerving. But don't let it be. These functions are simply additions
to our ``zoo'' of available functions. There actually are some inverse-trigonometric
identities, but they are not that useful and we will not worry about them.
So why study inverse trigonometric functions at all? Well, we want to be able
to integrate and differentiate just about every ``normal'' function we can.
I'm not considering inverse trig functions as ``normal'' in that sense. What
we will see today, though, is that the derivatives of these inverse trig functions
are algebraic, sometimes even rational functions, so in order to antidifferentiate
those functions, we need to talk about inverse trig functions.
The Inverse sine
sin-1 is the inverse of sin. By saying that, we have to
mean that, if you restrict the domain of sin(x) to the right interval
so that it is one-to-one, then there is an inverse, which we call sin-1(x) .
It is also called arcsin(x) or Arcsin(x) . Maple understands
arcsin(x) . Technically, sin-1(x) is defined by:
|
sin-1(x): = yÛ y Î [-p/2,p/2], and sin(y) = x. |
|
To find the derivative of sin-1(x) , we do as we did before: define
y to be y = sin-1(x) . Then we want dy/dx . By definition,
sin(y) = x , and so:
|
|
|
|
x. Now, differentiate implicitly: |
| |
|
| |
|
|
|
Here it is a little complicated to solve for dy/dx in terms of x
directly.
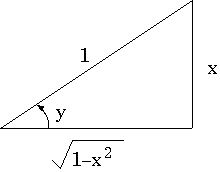 Think of a right triangle, with angle y . If sin(y) = x , then we
can choose our scale so that the hypotenuse is 1 (we divide by the hypotenuse
to find sin(y) , so we do want to have it be 1 to simplify the arithmetic).
Then, the opposite side to y has length x , since
Think of a right triangle, with angle y . If sin(y) = x , then we
can choose our scale so that the hypotenuse is 1 (we divide by the hypotenuse
to find sin(y) , so we do want to have it be 1 to simplify the arithmetic).
Then, the opposite side to y has length x , since
|
sin(y) = opp/hyp = x/1 = x. |
|
The formula above has cosx , however. You see that from the same picture,
So, substitute that for cos(y) and you have:
The Inverse cosine
You can think about how you define the inverse cosine, just as for sin-1 .
The only really new thing is the restriction on y , which can't be the
same as for sin-1 since it isn't one-to-one there.
|
cos-1(x): = yÛ y Î [0,p] and cos(y) = x. |
|
If you were to go through the calculations again, you would have that:
Since the derivatives are almost the same (they differ by just the sign), we
don't worry too much about cos-1x . Actually, there is an inverse-trigonometric
identity behind this.
The Inverse tangent
This one is perhaps easier. We start out as before:
|
tan-1(x): = yÛ y Î (-p/2,p/2) and tan(y) = x. |
|
And:
Now, look at the right triangle again, this time with the side opposite y
having length (by scaling) x , and the adjacent side 1 .
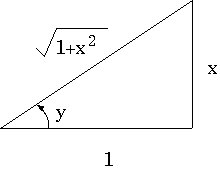 That puts the denominator in the equation tan(y) = opp/adj to 1, so we
can easily manipulate it. Now consider the formula above. Since cos(y) = adj/hyp ,
That puts the denominator in the equation tan(y) = opp/adj to 1, so we
can easily manipulate it. Now consider the formula above. Since cos(y) = adj/hyp ,
Plugging in to the equation above, and we're done:
The Inverse secant
Three more to go. Actually, though, after this one the rest of the inverse trig
functions will not give any new integration (antidifferentiation) formulas.
The reason is the same as for the inverse cosine. So, this is the last one.
|
sec-1(x): = yÛ y Î [0,p/2) or y Î [p,3p/2), and sec(y) = x. |
|
You should note that the domain here for sec-1(x) is a bit nonstandard
in the choice of domain.
And:
Here it is a little messier. For the right triangle with standard angle y ,
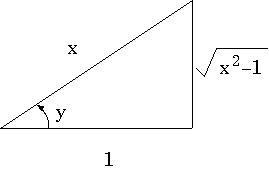 scaled so that the adjacent side is 1 (the denominator of sec(y) ), and
hypotenuse x , then sec(y) = x and
scaled so that the adjacent side is 1 (the denominator of sec(y) ), and
hypotenuse x , then sec(y) = x and
so
I must confess. I cheated. I described these pictures, with the right triangles
and all, forgetting that the domain of these functions include some x < 0 .
But there the geometry is invalid. You actually only have to see how the signs
of the trig functions change when x < 0 to see how to extend them. But
that is usually unneeded, since the signs won't change. For sec-1x ,
however, it matters.
for y Î [p,3p/2) . But then sec(y) = x as well, since both are negative. So, really:
Using a different domain for the definition of the inverse secant, such as y Î [0,p/2)È(p/2,p] ,
which is actually more common than the definition used here, then
Copyright (c) by David L. Johnson.
File translated from
TEX
by
TTH,
version 2.61.
On 22 Apr 2000, 18:53.