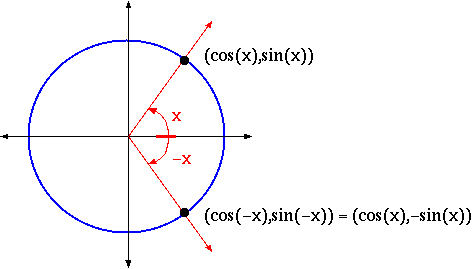On-line Math 21
On-line Math 21
3.1 Trigonometric functions
3.1.1 Basic definitions
This is intended to be a reminder of the basic properties of trigonometric functions.
It is too brief to replace a course in trigonometry, and it focuses on only
those properties of trigonometric functions that have particular use for calculus.
The classical uses of trigonometry, such as surveying and other tasks where
the measurement of various lengths and angles are the primary object, are not
developed. Also, the many trigonometric identities that comprise a large part
of most trigonometry courses are cut back to only those identities that are
useful for calculus.
Right triangles, adjacent sides, and so on.
Trigonometric functions are disconcerting to a number of students because they
are the first functions they see which are not really described algebraically.
They are a different sort of function, whose best description is through geometry.
The first definition is for the sine of an angle q, written sinq.
In order to even define sinq, you have to first construct a right
triangle with angle q, then label the sides opposite to
q, adjacent to q, and the hypotenuse.
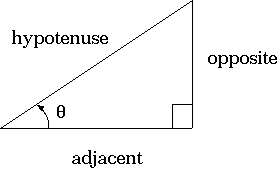 Then, sinq is defined as
Then, sinq is defined as
|
sinq: = |
opposite
hypotenuse
|
. |
|
There are 5 other trigonometric functions, the cosine ( cosq),
tangent ( tanq), cotangent ( cotq), secant ( secq),
and cosecant ( cscq). They can all be defined similarly to sinq,
according to the following table:
|
|
|
| |
|
| |
|
|
|
sinq
cosq
|
= |
opposite
adjacent
|
|
| |
|
|
|
cosq
sinq
|
= |
1
tanq
|
= |
adjacent
opposite
|
|
| |
|
|
|
1
cosq
|
= |
hypotenuse
adjacent
|
|
| |
|
|
1
sinq
|
= |
hypotenuse
opposite
|
. |
|
|
There are several things to point out about these definitions. The first is
that they are all ratios of sides of the triangle. The reason for that is that
these functions are not supposed to depend on the size of the triangle, only
on the size of the angle. From geometry, the ratios of sides are independent
of the size of the triangle, as long as the angles are the same. (as long as
the triangles are similar). The second thing to notice is that I listed
first the expressions of one trigonometric function in terms of others, if possible.
Always remember that any trigonometric function can be written in terms of sinq
and cosq.
Angles and the unit circle
While the previous paragraph is the first way you probably saw trigonometric
functions defined, it was not the best way. For our purposes we need to re-cast
the definitions in terms of the unit circle. Most importantly, we need these
functions to be functions of a real number, not an angle (or even an angle in
degrees).
Imagine an angle being represented by a ray from the origin. That ray makes
the angle q with the positive horizontal ( x ) axis. The radian
measure of the angle q is defined as the distance from the positive
x -axis to the ray along the unit circle, measured counter-clockwise.
The unit circle is the circle of points a distance 1 from the origin.
That circle is given by the equation x2+y2 = 1 .
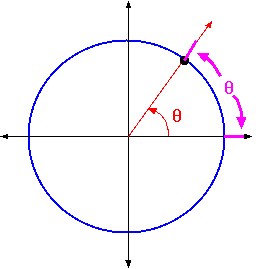 Now, the angle q can be either positive or negative (negative angles
correspond to measuring clockwise along the circle), and can have any value.
Get used to measuring angles in radians, rather than in degrees. The main reason
for this is that calculus of trigonometric functions works far better with radian
measure. In applications, as well, it is often convenient to use radian measure.
For most purposes, radian measure has no ``units'' of distance, since it can
be defined as the ratio of the arclength divided by the radius of the circle.
Of course, we take the circle to be the unit circle, so the radius is 1, but
as a ratio, radian measure can be used for circles of different radii.
Now, the angle q can be either positive or negative (negative angles
correspond to measuring clockwise along the circle), and can have any value.
Get used to measuring angles in radians, rather than in degrees. The main reason
for this is that calculus of trigonometric functions works far better with radian
measure. In applications, as well, it is often convenient to use radian measure.
For most purposes, radian measure has no ``units'' of distance, since it can
be defined as the ratio of the arclength divided by the radius of the circle.
Of course, we take the circle to be the unit circle, so the radius is 1, but
as a ratio, radian measure can be used for circles of different radii.
From the context of the unit circle, the functions cosq and sinq
of the angle q in radian measure (or, of the number q)
is defined as the x - and y -coordinates of the point where the
ray at angle q crosses the unit circle, x = cosq and
y = sinq.
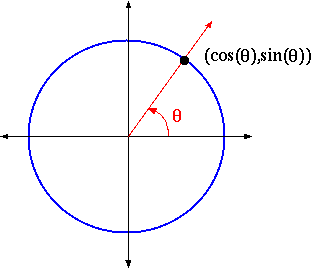 To find the values of the other trigonometric functions, you need to use the
table above, that is, to find tanq, use the fact that tanq = sinq/cosq.
In fact, most of the time we will only concentrate on sinq and
cosq, only using the others when they are needed for their special
properties. That does occur, though, since the calculus of tanq
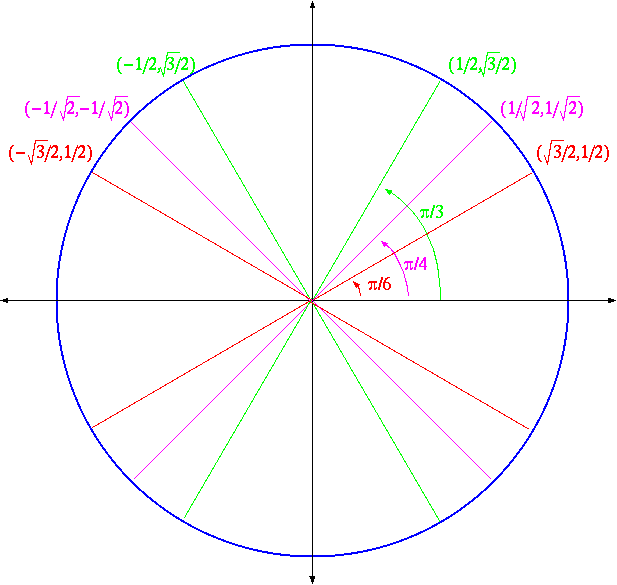
and secq has special twists. The following picture shows the
value of (cosq,sinq) for various values of q.
Only some of the values are filled in, but the pattern continues, with only
the signs changing for the other two quadrants.
To find the values of the other trigonometric functions, you need to use the
table above, that is, to find tanq, use the fact that tanq = sinq/cosq.
In fact, most of the time we will only concentrate on sinq and
cosq, only using the others when they are needed for their special
properties. That does occur, though, since the calculus of tanq
and secq has special twists. The following picture shows the
value of (cosq,sinq) for various values of q.
Only some of the values are filled in, but the pattern continues, with only
the signs changing for the other two quadrants.
sin(x) and cos(x) as functions.
Now we want to separate these trigonometric functions from the unit circle,
and think of them as functions. There is a source of confusion in doing this,
since we now will deal with sin(x) , where the x refers not to
the x -coordinate on the unit circle, but the number corresponding to
an angle of radian measure x . If we do have to think about the unit circle
explicitly, we will need a new label for the horizontal axis - probably calling
the axes the u and v axes makes it easier.
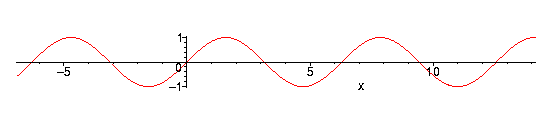
As a function, what does sin(x) look like? Since sin(x) is
the horizontal component of a point on the unit circle, then certainly it is
a number between -1 and +1 . Since sinq makes since
for any angle q, sin(x) is defined for all x . These
two observations say that sin(x) has domain the entire real line, and
range the interval [-1,1] . Following along the circle above, you can
see that the graph of y = sin(x) looks like the following:
 You should use Maple to plot, for various choices of domain x ,
all of the standard trigonometric functions: sin(x) , cos(x) ,
tan(x) , cot(x) , sec(x) , and csc(x) .
You should use Maple to plot, for various choices of domain x ,
all of the standard trigonometric functions: sin(x) , cos(x) ,
tan(x) , cot(x) , sec(x) , and csc(x) .
On thing you should notice is that the plots seem to be similar. In particular,
the graph of cos(x) is nearly the same as that of sin(x) .
In fact, they actually are the same, except that one is shifted to one side
from the other. The best way to see that shift is to think about the plot of
sin(x-a) , which is the function whose value at x is the same
as sin(x) has at x-a . So, the graph of sin(x-a) is
the same as that of sin(x) but shifted to the right by a
units. Try that in the following graphic, comparing the graph of sin(x)
to sin(x-a), and to cos(x), as you change a . Find the value of a for which sin(x-a) = cos(x).
[This should be a ``toy'' which
plots sin(x), cos(x) and sin(x-a) simultaneously, after the user chooses
the value for a ].
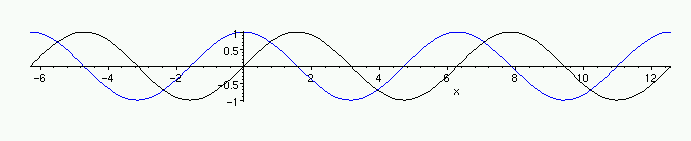
This ``shifting'' of the plot by a units to the right by replacing
x by (x-a) everywhere in the formula will of course work for all
functions, and you can see for example that cot(x) is a shift of tan(x)
and csc(x) is a shift of sec(x) .
Trigonometric identities
A trigonometric identity is a relationship between trig functions, such as
|
cos(x) = sin |
æ
ç
è
|
|
p
2
|
-x |
ö
÷
ø
|
, |
|
which holds for all values of x . Trigonometric identities account for
hundreds of pages, hundreds of different identities, in a trigonometry text.
We are not going to re-construct that here. We are, instead, going to concentrate
on a very few of these identities (some of which will be exercises), the ones
which are most important for calculus.
There are a number of easy identities that follow from the definitions of sinx
and cosx . For example, since -x is the same angle as x ,
but wrapped the other way around the unit circle,
which you can see from the drawing.
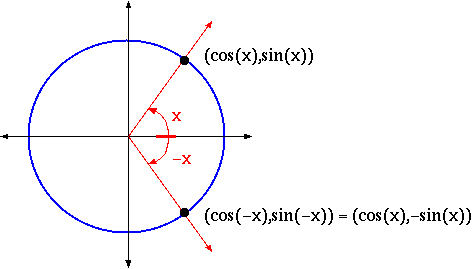 The absolutely most fundamental trigonometric identity is the equation that,
for any x ,
The absolutely most fundamental trigonometric identity is the equation that,
for any x ,
This means that, for any x, (sin(x))2+(cos(x))2 = 1 , but
it is always written this other way. We will always mean by sin2x
the number (sin(x))2 , and not the (bizarre) function sin(sin(x)) .
Where does this fundamental identity come from? Well, since (cos(x),sin(x))
is a point on the unit circle u2+v2 = 1 (remember, the axes of the
unit circle are u and v now), taking u = cos(x) and v = sin(x) ,
the equation of the circle is the same as cos2x+sin2x = 1 , which
is the same as the identity except that the order of the sum is reversed, which
doesn't matter.
This identity is used in countless ways, as we will see. The most common use
of it is to replace cosx , say, by
Why you would want to do that is another question, and will be clear when it
is needed. Many other identities are derived from it, such as
which is exactly the same identity, divided by cos2x , with the names
for the ratios sinx/cosx = tanx and 1/cosx = secx substituted
in.
There is one other (yes, really, only one) fundamental identity. All others
follow from this one, the ones we have already discussed, and the definitions
of the trig functions. That identity is the addition rule - well, it's really
two, since there are addition rules for sine and cosine.
|
|
|
|
sin(A)cos(B)+cos(A)sin(B) |
| |
|
| cos(A)cos(B)-sin(A)sin(B) |
|
|
We'll prove the second of these identities, by looking at a picture: Proof
Using these identities, you can (yes, you can) show that the following long
list of identities hold. Some are all set up as examples that you can work through.
|
cos(A+B) = cos(A)cos(B)-sin(A)sin(B) |
|
|
sin(A+B) = sin(A)cos(B)+cos(A)sin(B) |
|
|
cos(A-B) = cos(A)cos(B)+sin(A)sin(B) |
|
|
sin(A-B) = sin(A)cos(B)-cos(A)sin(B) |
|
|
tan(A+B) = |
tan(A)+tan(B)
1-tan(A)tan(B)
|
|
|
|
tan(A-B) = |
tan(A)-tan(B)
1+tan(A)tan(B)
|
|
|
|
cos(2x) = cos2(x)-sin2(x) |
|
The identity for cos(2x) generates, along with the fundamental identity
cos2(x)+sin2(x) = 1 , two more identities that are then used for
some additional identities that are very useful in calculus.
Solving for cos2(x) or sin2(x) gives
These lead, as well, to half-angle formulas (substituting t = 2x and taking
square roots)
Complementary angles and periodicity
The terms ``cosine'', ``cotangent'', and ``cosecant'' refer to the fact
that the cosine of an angle q is the same as the sine of the complementary
angle, the other angle of a right triangle. That is,
|
cos(q) = sin |
æ
ç
è
|
|
p
2
|
-q |
ö
÷
ø
|
, |
|
and so on. Those are another form of trigonometric identity, and can be verified
by applying the subtraction formulas where A = p/2 and B = q.
That is,
Similarly, because when you change from an angle with measure q
to q+2p, the ray from the origin does not change, any trig function
will be the same at q+2p as it was at q, that is,
This reflects the periodicity of trigonometric functions, the fact that, after
an interval of 2p, the function repeats its values from the previous
interval.
Copyright (c) by David L. Johnson, last modified
On 25 Apr 2000, 20:02..
File translated from
TEX
by
TTH,
version 2.61.
On 25 Apr 2000, 20:02.