On-line Math 21
On-line Math 21
3.3 Derivatives of ex and ln(x) .
3.3.1 Limits of exponential functions
Exponential functions always seem to involve this mysterious number e .
It's definition is wrapped up with limits and derivatives of exponential functions.
So, what's e ? The number e is chosen to be that one number so
that the exponential function with that as its base passes through (0,1) with
slope 1. Recall the picture of the various exponential graphs:
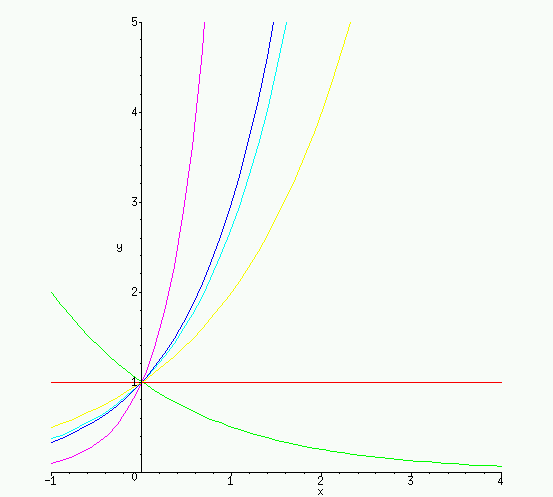That's really the primary reason why e is chosen as it is. It's similar
to the reason we use radian measure for trigonometric functions: things work
out more conveniently that way.
To see what makes the slope at (0,1) so important, look at the derivation of
the derivative of f(x) = ax , for an arbitrary a :
The last part,
is the slope of the curve y = ax at (0,1). If we can choose a
so that that last bit is 1, we really have simplified the situation. So, define
e to be that base for which the slope is 1, and you have a neater
formula. Does there exist such a base? Certainly you can find one with slope
0, or negative, and you can find one with huge slope at (0,1), like y = 1000x ,
so somewhere in between you can find one with slope 1. (This, by the way, uses
the Intermediate Value Theorem, which will be dealt with officially in the next
chapter). That base is e , and its value is 2.71828... Here is a picture
of just y = 2x, y = 3x, and y = x+1 . The last one
is a line with slope 1 going through (0,1). You should notice that y = 2x
does not have enough slope at (0,1), while y = 3x has too much.
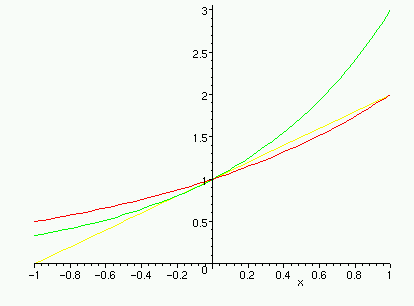Look back again at that derivation of the derivative of ax . It shows
that:
which seems odd, but is true. The slope at each value of x is the value
at that x . This property is important in using the exponential function
as a model of systems, but for now, that's just the derivative formula. From
now on, though, f(x) = ex is just another function to add to our list.
You use all the other derivative rules with this function like you any other
function.
3.3.2 Logarithms.
Logarithms are just exponents in reverse:
So, log42 = 1/2 , log3(1/3) = -1 , and so on. There is a special
case, when the base is e . Then, instead of writing logex ,
we write lnx , the natural logarithm of x . There is
also another notation for log10x . It is sometimes called logx ,
the common logarithm of x . Unfortunately, most post-calculus
math texts now confuse the notational issue even more, by writing the natural
logarithm of x as logx . Hopefully, it will be clear from the
context which is meant. To a mathematician, there is no special significance
of the number 10, except for the number of fingers we have.
The derivative of the natural logarithm is figured out by the using the fact
that the logarithm is the inverse of the exponential. Really, though, it's just
the chain rule: if f(x) = lnx , then
The text has a couple of other formulas that are really the same as this one,
but fancier-looking since they stick the chain rule in there:
|
( ln(g(x)) ¢ = |
g¢(x)
g(x)
|
, |
|
and
This last one looks like the same formula, except with the absolute value sign.
But remember that lnx itself is defined only for x > 0 , so this
is a way to extend it to x < 0 - sort of. For x < 0 , set u = -x ,
then, using the version with the chain rule:
So, the formula does work the same for either positive or negative values of
x .
Copyright (c) 2000 by David L. Johnson.
File translated from
TEX
by
TTH,
version 2.61.
On 23 May 2000, 18:22.