On-line Math 21

On-line Math 21

2.4  Applications of the derivative.

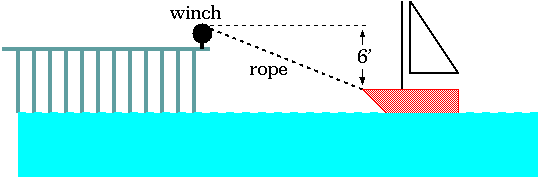
Example 1 A boater has his boat tied to the pier by a long rope. He feeds the pier-end of the rope through a winch and pulls his boat in towards the pier. The tide is out, so the bow of the boat is 6 feet below the level of the pier. If the winch is pulling in the line at a constant rate of 2 feet per second, how fast is the boat moving towards the pier when there is 10 feet of rope between the boat and the winch?

Solution

The first thing to do is to identify what information you know, what information you want (well, OK, what you are asked to find), and when. The ``when'' will usually be expressed in terms of the time when one or more of the quantities has a set value, but sometimes it is a certain time during the course of the problem.

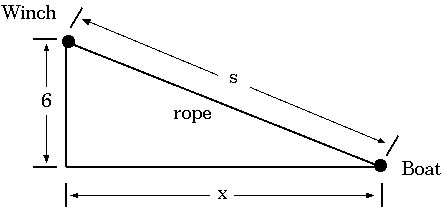
To do this, label with variables those quantities that vary. Only label as constants things that stay constant throughout. Also, as pretty as the animated graphics may be, it helps to reduce the drawing to the relevant essentials. Since the boat moves horizontally, the speed of the boat is the rate of change of the horizontal distance between the boat and the dock. Call that distance x . Of course, you should think of it as a function x(t) of time, but just label it as x . Similarly, call the length of the rope (between the winch and the bow) s . You need these variables because you need to know something about how x changes, and you know something about the rate of change of s . Of course, the distance down from the winch to the boat is a constant 6 feet.

Then, in this example, we:

Know

that ds/dt = -2 . It's negative because the length of the rope is decreasing. Note that we keep units consistent; here we make the natural choices that time is measured in seconds and distance in feet, since that is the way the problem is given,

Want

dx/dt

When

s = 10. Be careful. Don't label the length of the rope as ``10''. It is not constant, and only after you differentiate should you replace s by 10.

We display all this by this diagram

The horizontal path of the boat, the line described by the rope, and the vertical drop from the winch to the boat's path form a right triangle. That triangle gives the relationship between the variables as well, according to the Pythagorean theorem (which gets used a lot in these problems)
x2+62 = s2.
To find the relationship between the rates of change of these quantities, differentiate both sides of the equation:
2x dx
dt
 +0 = 2s ds
dt
 .
At this point you should be able to simply plug in the values of what you know: ds/dt = -2 . But you need more to solve for what you want ( dx/dt ). You of course plug in the when, but here the ``when'' only directly gives s = 10 , and you still can't solve for what you want, since there is that remaining x . To find x you re-use the relationship between the variables, this time plugging in for the when:
x2+62
=
s2
x2+36
=
100, so
x2
=
100-36 = 64, or
x
=
8.
Actually, if you remember your geometry there is an easier way to do this. This is a ``3-4-5'' triangle - well, a ``6-8-10'', but it's the same idea.

Aside

Now, plug in for x and s , as well as ds/dt, and solve for dx/dt :
x2+62
=
s2
2x dx
dt
 +0
=
2s ds
dt
2·8 dx
dt
=
2·10·(-2), or
dx
dt
=
-5
2
 .

Copyright (c) 2000 by David L. Johnson.

File translated from TEX by TTH, version 2.61.
On 24 Nov 2000, 17:43.