The idea of a limit is the fundamental distinction between calculus and all
the mathematics that is typically labelled ``precalculus''. Whether we're
dealing with the slope of a curve, the area of a region in the plane, or the
speed of a moving object, the fundamental idea will always be the same; we want
to find what the value of some function f(x) ought to be at
a specific point a , based on its value at all nearby points. That's what
a limit is, what the value of the function should be at the specific point.
We say that that ``proper'' value is the limit of the function
f(x) as x approaches the point a , or
|
As a specific example, let's look at the function
|

But that seems silly. All I have to do is divide out the top and bottom by (x-1) and it would be defined. Well, there will be other examples where that isn't so easy, so let's pretend we didn't see that.
What should f(1) be? Well, the way I want to see that is to
look at various values of f(x) for x near 1, and see where things
are heading. here's a small table:
|
I think I get the pattern. Of course, f(1) ought to be 2. But, you can see that just by knowing the values of the function, as x gets closer and closer to 2, without knowing how to simplify the expression so that the division by 0 doesn't appear. Most serious examples of this idea won't be simple enough so that you can just divide out and have it become obvious.
We write the result of this ``investigation'' as
|
We need a formal definition of a limit. However, the really formal definition seems to have a lot of excess baggage that comes with it. It is needed, of course, but it is confusing at first. So, we'll start out with a slightly informal definition:
Definition 1
If f is a function defined on an interval (c,a) , and on (a,b) ,
then we say that the limit of f(x) as x approaches a , is
L , written
For the formal, rigorous, definition, look at the official definition.
if we can be sure that f(x) is as close as we need to L , by just
taking x close enough to a .
lim
x® a
f(x) = L,
Remark 2
Note that the function doesn't have to be defined at a , but
it does need to be defined at all points sufficiently close to a
on either side. It can be the case that the function is defined at a ,
but that might not be the limit L .
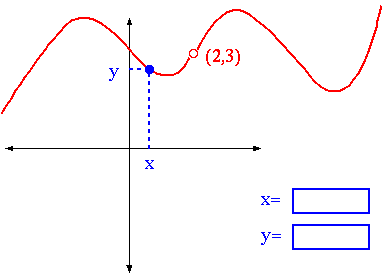
Here is an example to show the idea of the limit. Even though, technically,
the function represented by this graph is not defined at x = 2 , the closer
you take x to 2 (click on a point of the graph), the closer y
gets to 3 .
Example 1
Let f(x) = 3x2+1 . Then
lim
x® 2
f(x) = Answer
Example 2
Let
Then
f(x) =
ì
í
î
3x+1
if x ³ 1
x+2
if x < 1
.
lim
x® 1
f(x) = Answer
Example 3
Let
Then
f(x) =
ì
í
î
x2
if x ¹ 1
5
if x = 1
.
lim
x® 1
f(x) = Answer
Example 4
Let f(x) = sin(1/x) . Then
lim
x® 0
f(x) Answer
Example 5
Let
Then
f(x) =
x3+1
x2-1
.
lim
x® -1
f(x) = Answer
Copyright (c) 2000 by David L. Johnson.