On-line Math 21

1.1  Functions

Calculus deals almost always with ``functions''. Although the term has different meanings in other situations, in mathematics a function y = f(x) , or just f , is always defined as the assignment, to each x in a set called the domain of the function, a value y in what is called the range of the function. To each x there is one and only one y . To indicate the domain A and the range B of f (we often leave out the (x) when we refer to a function), we sometimes write f:A® B .

The reason we want to leave out the (x) of a function f , calling it by just the letter f rather than f(x) , is sometimes confusing. Let's say we define a function f by a formula, say f(x) = x² . That means, to each number x , this function assigns its square. You write a particular case of that, say the value when x = 2 (that value is 4, of course), by writing f(2) = 4 . Really, we should write f( ) for the function itself, but we leave out the parentheses.

We can also replace the x by another letter, so for this same function f(x) = x² , f(t) makes sense, and f(t) = t² .

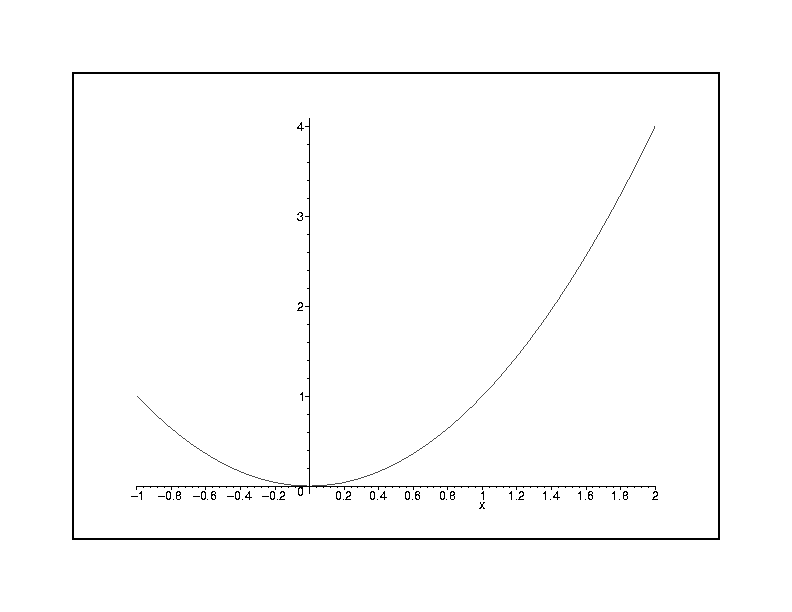
There is some confusion between the function f itself and its graph. The graph of a function f(x) = x² , for x in a specified domain (say from -1 to 2), is the set of points (x,f(x)) in the plane where x Î [-1,2] , that is, the set of points (x,y) where x Î [-1,2] and for each such x , the y is that one y satisfying y = f(x) = x² . Here is the picture:

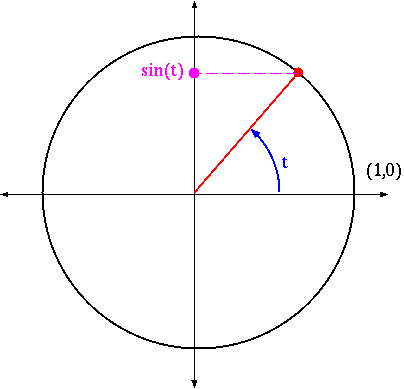
Depending on the information available, a function can be described in a number of different ways. The current text lists four distinct ways, but with a little imagination you could probably come up with more. You've already seen functions defined by formulas (or algebraically), and graphs. A function can also be described verbally, such as the following: For each t , f(t) is the y -coordinate of the point on the circle of radius 1, centered at the origin, at an angle t from the positive x -axis. In this case, f(t) = sin(t) . This verbal description may seem difficult (it was, in a sense, meant to be), but if you look at the picture you see that, indeed, sin(t) is exactly the y -coordinate of the point on the unit circle at an angle t from the positive x -axis.

Another way that functions are often defined for calculus texts, which you rarely see elsewhere, is ``piecewise'', that is, for some part of the domain f is defined by one formula, and in other parts of the domain f has another formula. We write these functions with a brace, indicating which formula is used for which parts of the domain. An example would be:

f(x): = ì í î 1-x, if x £ 1 x2, if x > 1.

Some of these ``piecewise'' functions you have seen before, such as the absolute value function g(x) = |x| . Since |x| is the same as x for x ³ 0 , but |x| is the opposite sign for x < 0, (erase the negative sign by adding another) so

g(x) = |x|: = ì í î x, if x ³ 0 -x, if x < 0.

piecewise-defined functions allow us to think about a lot of properties of functions that you don't see when you only deal with functions defined by a single formula.

More properties of functions

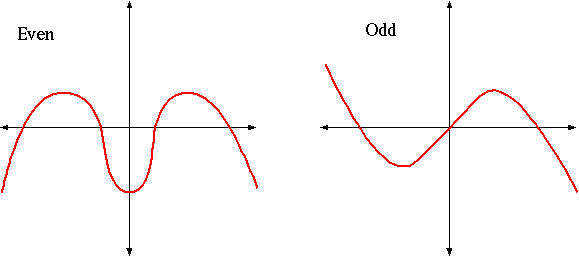
Some functions have special properties that make them easier to understand. The first notion is that of symmetry (even or odd functions). A function f(x) is even if f(-x) = f(x) , and is odd if f(-x) = -f(x) . An even function has mirror symmetry with respect to reflection about the y -axis, and an odd function has ``flipped'' symmetry, or is symmetric with respect to the origin.

0.6  Standard functions

Copyright (c) 2000 by David L. Johnson.