On-line Math 21

1.1 Achilles and the Tortoise - Sequences and Series

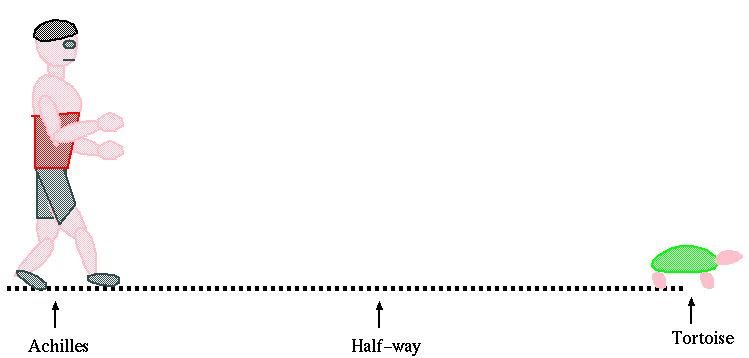
I always begin a discussion of series and sequences (these two topics are really one idea, viewed from two different sides) with Greek mythology. This keeps alive the belief that we are fostering liberal education.

Today's myth is that of Achilles and the tortoise. The story is, for reasons that I'll never figure out, they are going to have a race. (This is also told with a hare in the role of Achilles, but then it doesn't seem so Greek.) The paradox involved in this story is that, assuming Achilles gives the tortoise a head start, which is only fair, he can never win, since in order to cover the distance from Achilles to the tortoise (the head start), Achilles must first go half that distance, then half the remaining distance, and then half of that, et cetera, so that he has to do infinitely many things in order to catch up to the tortoise.

As with all the Greek paradoxes, this has an explanation. Let's assume that the distance from Achilles to the tortoise is 1 mile. Then, in order to get to the tortoise, Achilles must first go a distance 1/2 mile, which would take him, say, 2 minutes. He then has to go the next 1/4 mile, which would take 1 minute, then the next 1/8 mile, taking 1/2 minute, then the next 1/16 mile, taking 1/4 minute, et cetera.

So, adding this all up, he has to run:

1/2+1/4+1/8+1/16+... miles,

which takes:

2+1+1/2+1/4+... minutes.

These totals may seem infinite, since they do go on forever, like some demented math professor, but they actually do approach a finite value as a limit.

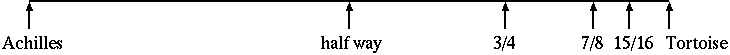
When you think about it, Achilles only has to run the one mile (the tortoise hasn't even taken a step yet), which is 1/2+1/4+1/8+... = 1 , and it takes 2+1+(1/2+1/4+... ) = 4 minutes (he is fast). There is really no paradox, since the infinitely many things he has to do can be done infinitely fast at the end.

File translated from T_EX by T_TH, version 2.61.
On 25 Sep 2000, 23:54.