My Commute

In the morning, I park on what Lehigh calls the "Mountaintop Campus" which is, as the name suggests, at the top of the hills that most of the campus lies on. It used to be Bethlehem Steel's research facility, but Lehigh bought it in the late '80's when the Steel was not doing so well. At any rate, parking is easy and convenient there, and it's close enough in to not add too much time to my commute.

I get the bike out of the car and ride down to my office, on the bottom of the hill (near Packer Avenue, in Christmas-Saucon Hall). That is no exercise at all; I could basically coast the whole way, though I tend to spin down much of it to practice downhilling. I then arrive in my office a bit windblown, but not all sweaty in need of a shower and clean clothes.

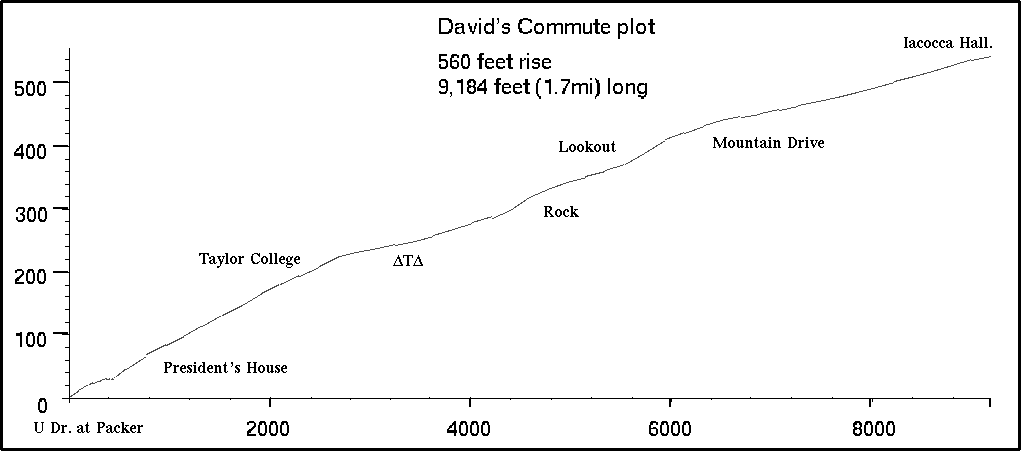
The afternoon is a bit more serious. As the graph shows, it's about 540 feet of climb in 1.7 miles. The first time I tried it, one of the graduate students in the department asked where to send the body. I didn't actually die, but I felt close. I did not make it without stopping, and that was on a reasonably small gear, a 42x24. Eventually I got to where I could do it, but it was discouraging, since I always was best at hill-climbing, and never rode with anything smaller than a 42x18 when I was really in shape. But that was then. I now can make it reasonably using nothing lower than a 35x20, and it takes me about 16-17 minutes. We'll see if I can improve that time.

Here's the graph of the hill. Of course, it's two-dimensional with all the turns leveled out. It's also not the same scale horizontally and vertically, but that was what Maple (a computer-algebra program I use) gave me. Here's a link to a map showing the route I take.

I have now found some more accomodating gears. I got a new crankset at the Trexlertown Velodrome annual flea market, a Campagnolo Victory set with a 51 and 35 chainrings. That is much wider than most people have, and makes the best (IMO) crossover-gear setup I have seen. I now have a 13-20 8-speed cluster, giving me lots of smaller gears.

Late last Fall, just before the Christmas break, I walked up my route, taking measurements every 100 paces or so of the slope (I had a 4-foot level and a measuring tape to find the slope). I then used those slope measurements to construct a function representing the slope (this was a cubic spline on the input data). My idea was to simply integrate this spline to get a graph of the curve itself, but Maple could not handle integrating the spline -- which it created. Thanks to Helmut Kahovec, Robert Israel, and others on sci.math.symbolic, I was given code to enable Maple to handle large data-set splines. It really ought to do that on its own, but that is another story.

The mathematics and mechanics of this is explained in The mathematics of my commute plot.

By the way, when people talk about the grade of a hill, they usually refer to it as a percentage. Now, that can either mean, say, that a 10% grade rises one foot for every 10 feet of travel along the road, or it could mean one foot rise for every 10 feet horizontally. The latter is correct, technically, although for most purposes it doesn't matter. Any hill steep enough so that the two ratios (the sine versus the tangent of the angle of inclination, respectively) will be too steep to climb.